题目内容

4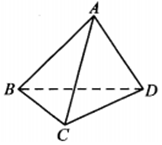．在四面体ABCD中，二面角A-BC-D为60°，点P为直线BC上一动点，记直线PA与平面BCD所成的角为θ，则（　　）
A．θ的最大值为60°B．θ的最小值为60°C．θ的最大值为30°D．θ的最小值为30°

分析 作出二面角和线面角，根据利用三角函数的定义表示出AO即可得出θ和60°的大小关系．

解答 解：过A作AM⊥BC，AO⊥平面BCD，垂足为O，连结OM，
则∠AMO为二面角A-BC-D的平面角，∴∠AMO=60°，
在直线BC上任取一点P，连结OP，AP，
则∠APO为直线AP与平面BCD所成的角，即∠APO=θ，
∵AP≥AM，AM•sin60°=AO，AP•sinθ=AO，
∴sinθ≤sin60°，即θ的最大值为60°．
故选A．

点评 本题考查了空间角的定义，作出空间角表示出棱锥的高是关键，属于中档题．

练习册系列答案
相关题目
14．P为抛物线x2=-4y上一点，A（2$\sqrt{2}$，0），则P到此抛物线的准线的距离与P到点A的距离之和的最小值为3．
15．已知数列{an}的前n项和为Sn，且a1=1，an+1=$\left\{\begin{array}{l}{{a}_{n}+3，\frac{n}{3}∉{N}^{*}}\\{{a}_{n}，\frac{n}{3}∈{N}^{*}}\end{array}\right.$若S3n≤λ•3n-1恒成立，则实数λ的取值范围为[14，+∞）．
12．等差数列{an}中，已知a1=-1，S19=0，则使an＞0的最小正整数n为11．
19．已知△ABC中，D在边BC上，且BD=4，DC=2，∠B=60°，∠ADC=150°．
（1）求AC的长；
（2）求△ABC的面积．
9．数列{an}的各项均为正数，且an+1=an+$\frac{2}{{a}_{n}}$-1（n∈N*），{an}的前n项和是Sn．
（Ⅰ）若{an}是递增数列，求a1的取值范围；
（Ⅱ）若a1＞2，且对任意n∈N*，都有Sn≥na1-$\frac{1}{3}$（n-1），证明：Sn＜2n+1．
16．已知sinx-cosx=$\frac{1}{5}$，0≤x≤π，则sin（2x+$\frac{π}{4}$）的值为$\frac{17\sqrt{2}}{50}$．
13．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+x，}&{x＜0}\\{-\frac{1}{x}，}&{x＞0}\end{array}\right.$的图象上存在不同的两点A、B，使得曲线y=f（x）在这两点处的切线重合，则点A的横坐标的取值范围可能是（　　）
A．（-$\frac{1}{2}$，0）B．（-1，-$\frac{1}{2}$）C．（$\frac{1}{2}$，1）D．（1，2）
12．若α是第二象限角，则$\frac{1}{2}$+$\frac{1}{2}$$\sqrt{\frac{1}{2}+\frac{1}{2}cos2α}$的值等于（　　）
A．cos2$\frac{α}{2}$B．sin2$\frac{α}{2}$C．cos2αD．sin2α

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网