题目内容
用1、5、9、13中任意一个数作分子,4、8、12、16中任意一个数作分母,可构成 个不同的分数?可构成 个不同的真分数?
考点:计数原理的应用
专题:排列组合
分析:用1、5、9、13中任意一个数作分子,4、8、12、16中任意一个数作分母,根据分步计数原理即可得到,
解答:
解:用1、5、9、13中任意一个数作分子,4、8、12、16中任意一个数作分母,有
•
=16个不同的分数,根据真分数的定义,每一个数字为一类,根据分类计数原理可得.
根据真分数的定义,
当分子为为1时,分母有4种选择,
当分子为为5时,分母有3种选择,
当分子为为9时,分母有2种选择,
当分子为为13时,分母有1种选择,
根据分类计数原理得真分数有,4+3+2+1=10种,
故答案为:16,10
| C | 1 4 |
| C | 1 4 |
根据真分数的定义,
当分子为为1时,分母有4种选择,
当分子为为5时,分母有3种选择,
当分子为为9时,分母有2种选择,
当分子为为13时,分母有1种选择,
根据分类计数原理得真分数有,4+3+2+1=10种,
故答案为:16,10
点评:本题主要考查了分类和分步计数原理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知定义在R上的函数f(x)满足f(x)•f(x+
π)=-1.若f(
)=2,则f(11π)等于( )
| 3 |
| 2 |
| π |
| 2 |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
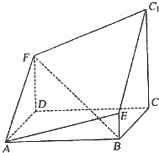 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1