题目内容
20.在△ABC中,A,B,C的对边分别为a、b、c,$C=\frac{π}{3},b=8$,△ABC的面积为$10\sqrt{3}$.(Ⅰ)求c的值;
(Ⅱ)求cos(B-C)的值.
分析 (Ⅰ)由已知利用三角形面积公式可求a的值,进而利用余弦定理可求c的值.
(Ⅱ)由(Ⅰ)利用余弦定理可求cosB的值,结合范围B∈(0,π),利用同角三角函数基本关系式可求sinB,进而利用两角差的余弦函数公式计算求值得解.
解答 (本题满分为12分)
解:(Ⅰ)∵$C=\frac{π}{3},b=8$,△ABC的面积为$10\sqrt{3}$=$\frac{1}{2}$absinC=$\frac{1}{2}×a×8$×sin$\frac{π}{3}$,解得:a=5,
∴由余弦定理可得:c=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{25+64-2×5×8×\frac{1}{2}}$=7…6分
(Ⅱ)∵由(Ⅰ)可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{49+25-64}{70}$=$\frac{1}{7}$,
又∵B∈(0,π),可得:sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{4\sqrt{3}}{7}$,
∴cos(B-C)=cosBcos$\frac{π}{3}$+sinBsin$\frac{π}{3}$=$\frac{4\sqrt{3}}{7}$×$\frac{\sqrt{3}}{2}$+$\frac{1}{7}×\frac{1}{2}$=$\frac{13}{14}$…12分
点评 本题主要考查了三角形面积公式,余弦定理,同角三角函数基本关系式,两角差的余弦函数公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
10.某校数学兴趣小组在研究本地的城市道路与汽车保有量之间的关系(即某地区道路的总里程数和该地区拥有的汽车数量之间的关系)时,得到了近8年的城市道路总里程x(单位:百公里)和汽车保有量y(单位:百辆)的数据如下表:
(Ⅰ)若某年的两个值都不小于170时,我们将该年称为“出行便捷年”.现从这8年中任取5年,求恰有2年为“出行便捷年”的概率(请用分数作答).
(Ⅱ)根据上表数据,用变量y和x的相关系数说明y与x之间线性相关关系的强弱.如果具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
参考公式:相关系数$r=\frac{{\sum_{i=1}^8{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}\sum_{i=1}^8{{{({y_i}-\overline y)}^2}}}}}$;回归直线的方程是:$\hat y=\hat bx+a$,
其中$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-\hat b\overline x$,${\hat y_i}$是与xi对应的回归估计值.
参考数据:$\overline x=155$,$\overline y=169.75$,$\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}=4200$,$\sum_{i=1}^8{{{({y_i}-\overline y)}^2}}=1827.5$,$\sum_{i=1}^8{({x_i}-\overline x)({y_i}-\overline y)}=2750$,$\sqrt{4200}≈64.80$,$\sqrt{1827.5}≈42.75$.
| 数据编号 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 道路里程数x | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 |
| 汽车保有量y | 144 | 154 | 160 | 168 | 176 | 180 | 186 | 190 |
(Ⅱ)根据上表数据,用变量y和x的相关系数说明y与x之间线性相关关系的强弱.如果具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
参考公式:相关系数$r=\frac{{\sum_{i=1}^8{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}\sum_{i=1}^8{{{({y_i}-\overline y)}^2}}}}}$;回归直线的方程是:$\hat y=\hat bx+a$,
其中$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-\hat b\overline x$,${\hat y_i}$是与xi对应的回归估计值.
参考数据:$\overline x=155$,$\overline y=169.75$,$\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}=4200$,$\sum_{i=1}^8{{{({y_i}-\overline y)}^2}}=1827.5$,$\sum_{i=1}^8{({x_i}-\overline x)({y_i}-\overline y)}=2750$,$\sqrt{4200}≈64.80$,$\sqrt{1827.5}≈42.75$.
8.已知集合$A=\{x|\frac{x+3}{x-3}≤0\}$,B={x|x-1≥0},则A∩B为( )
| A. | [1,3] | B. | [1,3) | C. | [-3,∞) | D. | (-3,3] |
15.将函数$y=2sin(2x+\frac{π}{6})$的图象向右平移$\frac{1}{4}$个周期后,所得图象对应的函数为f(x),则函数f(x)的单
调递增区间( )
调递增区间( )
| A. | $[kπ-\frac{π}{12},kπ+\frac{5π}{12}](k∈Z)$ | B. | $[kπ+\frac{5π}{12},kπ+\frac{11π}{12}](k∈Z)$ | ||
| C. | $[kπ-\frac{5π}{24},kπ+\frac{7π}{24}](k∈Z)$ | D. | $[kπ+\frac{7π}{24},kπ+\frac{19π}{24}](k∈Z)$ |
9.设集合A={-1,1},集合B={x|ax=1,a∈R},则使得B⊆A的a的所有取值构成的集合是( )
| A. | {0,1} | B. | {0,-1} | C. | {1,-1} | D. | {-1,0,1} |
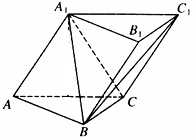 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,