题目内容
9.设集合A={-1,1},集合B={x|ax=1,a∈R},则使得B⊆A的a的所有取值构成的集合是( )| A. | {0,1} | B. | {0,-1} | C. | {1,-1} | D. | {-1,0,1} |
分析 利用B⊆A,求出a的取值,注意要分类讨论.
解答 解:∵B⊆A,
∴①当B是∅时,可知a=0显然成立;
②当B={1}时,可得a=1,符合题意;
③当B={-1}时,可得a=-1,符合题意;
故满足条件的a的取值集合为{1,-1,0}
故选:D.
点评 本题主要考查利用集合子集关系确定参数问题,注意对集合B为空集时也满足条件.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
17.执行如图所示的程序框图,输出S的值为( )


| A. | 45 | B. | 55 | C. | 66 | D. | 110 |
14.已知集合A={1,2,3},B={2,3},则( )
| A. | A∩B=∅ | B. | ∁AB=B | C. | A⊆B | D. | B$\begin{array}{l}?\\≠\end{array}$A |
1.过双曲线$\frac{x^2}{3}-{y^2}=1$右焦点的直线l被圆x2+(y+2)2=9截得弦长最长时,则直线l的方程为( )
| A. | x-y+2=0 | B. | x+y-2=0 | C. | x-y-2=0 | D. | x+y+2=0 |
18.已知函数f(x)=|lnx|,若在区间$[\frac{1}{3},3]$内,曲线g(x)=f(x)-ax与x轴有三个不同的交点,则实数a的取值范围是( )
| A. | $[\frac{ln3}{3},\frac{1}{e})$ | B. | $[\frac{ln3}{3},\frac{1}{2e})$ | C. | $(0,\frac{1}{e})$ | D. | $(0,\frac{1}{2e})$ |
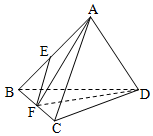 在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④
在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④