题目内容
11.在数列{an}中,a1=3,a17=67,通项公式是关于n的一次函数.(1)求数列{an}的通项公式;
(2)求a2013;
(3)2015是否为数列{an}中的项?若是,为第几项?
分析 (1)设an=kn+b(k≠0),由已知得$\left\{\begin{array}{l}{k+b=3}\\{17k+b=67}\end{array}\right.$,从而能求出an=4n-1.
(2)由an=4n-1,能求出a2013.
(3)令2015=4n-1,能求出2015是数列{an}的第503项.
解答 解:(1)设an=kn+b(k≠0),
∵a1=3,a17=67,
∴$\left\{\begin{array}{l}{k+b=3}\\{17k+b=67}\end{array}\right.$,解得k=4,b=-1.
∴an=4n-1.
(2)∵an=4n-1,
∴a2013=4×2013-1=8051.
(3)令2015=4n-1,解得n=504∈N*,
∴2015是数列{an}的第504项.
点评 本题考查等差数列的性质的应用,是基础题,解题时要认真审题.

练习册系列答案
相关题目
1.若实数x,y满足不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x+2y-2≥0}\\{y≥0}\end{array}\right.$,则z=3x+2y+1的最小值为( )
| A. | 2 | B. | 3 | C. | 6 | D. | 7 |
3.已知圆的方程为x2+y2-6x=0,过点(1,2)的该圆的所有弦中,最短弦的长为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
1.过双曲线$\frac{x^2}{3}-{y^2}=1$右焦点的直线l被圆x2+(y+2)2=9截得弦长最长时,则直线l的方程为( )
| A. | x-y+2=0 | B. | x+y-2=0 | C. | x-y-2=0 | D. | x+y+2=0 |
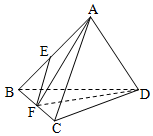 在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④
在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④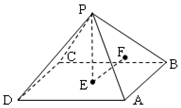 如图,P-ABCD是棱长均为1的正四棱锥,顶点P在平面ABCD内的正投影为点E,点E在平面PAB内的正投影为点F,则 tan∠PEF=$\sqrt{2}$.
如图,P-ABCD是棱长均为1的正四棱锥,顶点P在平面ABCD内的正投影为点E,点E在平面PAB内的正投影为点F,则 tan∠PEF=$\sqrt{2}$.