题目内容
8.已知集合$A=\{x|\frac{x+3}{x-3}≤0\}$,B={x|x-1≥0},则A∩B为( )| A. | [1,3] | B. | [1,3) | C. | [-3,∞) | D. | (-3,3] |
分析 分别求出集合A和B,由此能求出A∩B.
解答 解:∵集合$A=\{x|\frac{x+3}{x-3}≤0\}$={x|-3≤x<3},
B={x|x-1≥0}={x|x≥1},
∴A∩B={x|1≤x<3}=[1,3).
故选:B.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集性质的合理运用.

练习册系列答案
相关题目
3.已知圆的方程为x2+y2-6x=0,过点(1,2)的该圆的所有弦中,最短弦的长为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
13.已知$a={(\frac{1}{3})^{\frac{1}{2}}},b={log_{\frac{1}{2}}}\frac{1}{3},c={log_3}\frac{1}{2}$则( )
| A. | C>b>a | B. | b>c>a | C. | b>a>c | D. | a>b>c |
17.执行如图所示的程序框图,输出S的值为( )


| A. | 45 | B. | 55 | C. | 66 | D. | 110 |
18.已知函数f(x)=|lnx|,若在区间$[\frac{1}{3},3]$内,曲线g(x)=f(x)-ax与x轴有三个不同的交点,则实数a的取值范围是( )
| A. | $[\frac{ln3}{3},\frac{1}{e})$ | B. | $[\frac{ln3}{3},\frac{1}{2e})$ | C. | $(0,\frac{1}{e})$ | D. | $(0,\frac{1}{2e})$ |
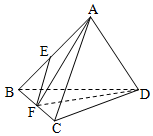 在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④
在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④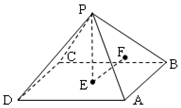 如图,P-ABCD是棱长均为1的正四棱锥,顶点P在平面ABCD内的正投影为点E,点E在平面PAB内的正投影为点F,则 tan∠PEF=$\sqrt{2}$.
如图,P-ABCD是棱长均为1的正四棱锥,顶点P在平面ABCD内的正投影为点E,点E在平面PAB内的正投影为点F,则 tan∠PEF=$\sqrt{2}$.