题目内容

7．已知函数y=f（x）的图象如图，则${f^'}（{x_A}）与{f^'}（{x_B}）$的关系是：（　　）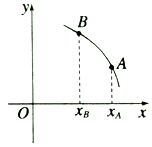
A．${f^'}（{x_A}）＞{f^'}（{x_B}）$B．${f^'}（{x_A}）＜{f^'}（{x_B}）$C．${f^'}（{x_A}）={f^'}（{x_B}）$D．不能确定

分析 根据导数的几何意义，判断在A，B两处的切线斜率即可得到结论．

解答 解：由图象可知函数在A处的切线斜率小于B处的切线斜率，
∴根据导数的几何意义可知f′（xA）＜f′（xB），
故选：B．

点评 本题主要考查导数的几何意义，根据导数和切线斜率之间的关系是解决本题的关键，比较基础．

练习册系列答案
相关题目
17．已知P是曲线y=$\frac{1}{4}$x2-$\frac{1}{2}$lnx上的动点，Q是直线y=$\frac{3}{4}$x-1上的动点，则PQ的最小值为$\frac{2-2ln2}{5}$．
18．在底面半径为2母线长为4的圆锥中内接一个高为x的正四棱柱，
（1）用x表示正四棱柱的侧面积；
（2）x为何值时，正四棱柱的侧面积最大？
15．当x+y+z=1时，则x2+y2+z2的最小值为（　　）
A．$\frac{1}{3}$B．$\frac{1}{9}$C．$\frac{1}{27}$D．3
2．已知函数f（x）的导函数为f′（x），且满足$f（x）=2x{f^'}（1）+\frac{1}{x}$，则f′（1）=1．
12．下面的茎叶图记录了甲、乙两名同学在10次英语听力比赛中的成绩（单位：分），已知甲得分的中位数为76分，乙得分的平均数是75分，则下列结论正确的是（　　）
A．$\overline{x_甲}=76，\overline{x_乙}=75$B．乙同学成绩较为稳定
C．甲数据中x=3，乙数据中y=6D．甲数据中x=6，乙数据中y=3
19．已知向量$\overrightarrow m=（\sqrt{3}sinx，sinx），\overrightarrow n=（cosx，sinx）$．
（Ⅰ）若$\overrightarrow m∥\overrightarrow n$且$x∈[{0，\frac{π}{2}}]$，求角x；
（Ⅱ）若$f（x）=\overrightarrow{m•}\overrightarrow n$，求函数f（x）的最小正周期和单调递增区间．
16．函数$f（x）=\frac{1}{x^2}+2x（x＞0）$的最小值为（　　）
A．3B．4C．5D．6
17．已知f（α）=$\frac{{sin（π-α）cos（2π-α）sin（-α+\frac{3π}{2}）}}{tan（-α-π）sin（-π-α）cos（-π+α）}$；
（1）化简f（α）；
（2）若α的终边在第二象限，$sinα=\frac{3}{5}$，求f（α）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网