题目内容
2.已知函数f(x)的导函数为f′(x),且满足$f(x)=2x{f^'}(1)+\frac{1}{x}$,则f′(1)=1.分析 首先对已知等式求导,然后令x=1,解得x值.
解答 解:$f(x)=2x{f^'}(1)+\frac{1}{x}$,则f'(x)=2f′(1)-$\frac{1}{{x}^{2}}$,
令x=1得到f'(1)=2f'(1)-1,解得f'(1)=1;
故答案为:1.
点评 本题考查了导数的运算以及方程思想求导数值;属于基础题.

练习册系列答案
相关题目
12.已知数列{an}的前n项和为Sn,a1=1,2Sn=an+1,则an+1=( )
| A. | 2n-1 | B. | 2n-1 | C. | 2×3n-1. | D. | $\frac{1}{2}({{3^n}-1})$ |
13.已知角θ在第二象限,且$|{sin\frac{θ}{2}}|=-sin\frac{θ}{2}$,则 $\frac{θ}{2}$在( )
| A. | 第一象限或第三象限 | B. | 第二象限或第四象限 | ||
| C. | 第三象限 | D. | 第四象限 |
7.已知函数y=f(x)的图象如图,则${f^'}({x_A})与{f^'}({x_B})$的关系是:( )
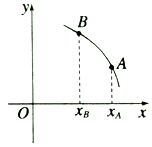

| A. | ${f^'}({x_A})>{f^'}({x_B})$ | B. | ${f^'}({x_A})<{f^'}({x_B})$ | C. | ${f^'}({x_A})={f^'}({x_B})$ | D. | 不能确定 |
11.已知角α的始边为x轴的正半轴,点(1,3)是角α终边上的一点,则tanα=( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
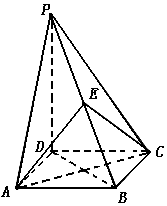 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.