题目内容
16．函数$f（x）=\frac{1}{x^2}+2x（x＞0）$的最小值为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 将函数解析式化为f（x）=$\frac{1}{{x}^{2}}$+x+x，运用基本不等式求最小值．
解答 解：$f（x）=\frac{1}{x^2}+2x（x＞0）$=$\frac{1}{{x}^{2}}+x+x≥3\root{3}{\frac{1}{{x}^{2}}•x•x}=3$，当且仅当$\frac{1}{{x}^{2}}=x$时等号成立；
故选A．
点评 本题考查了基本不等式的应用；关键是将函数式化为运用基本不等式的形式．
练习册系列答案
阅读快车系列答案
相关题目
7．已知函数y=f（x）的图象如图，则${f^'}（{x_A}）与{f^'}（{x_B}）$的关系是：（ ）
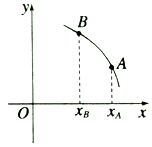
| A． | ${f^'}（{x_A}）＞{f^'}（{x_B}）$ | B． | ${f^'}（{x_A}）＜{f^'}（{x_B}）$ | C． | ${f^'}（{x_A}）={f^'}（{x_B}）$ | D． | 不能确定 |
11．已知角α的始边为x轴的正半轴，点（1，3）是角α终边上的一点，则tanα=（ ）
| A． | -3 | B． | -$\frac{1}{3}$ | C． | $\frac{1}{3}$ | D． | 3 |
6．若函数$f（x）=2sin（ωx+\frac{π}{4}）（ω＞0）$与$g（x）=2cos（2x-\frac{π}{4}）（ω＞0）$的对称轴完全相同，则函数$f（x）=2sin（ωx+\frac{π}{4}）（ω＞0）$在[0，π]上的一个递增区间是（ ）
| A． | $[0，\frac{π}{8}]$ | B． | $[0，\frac{π}{4}]$ | C． | $[\frac{π}{8}，π]$ | D． | $[\frac{π}{4}，π]$ |