题目内容
19.已知向量$\overrightarrow m=(\sqrt{3}sinx,sinx),\overrightarrow n=(cosx,sinx)$.(Ⅰ)若$\overrightarrow m∥\overrightarrow n$且$x∈[{0,\frac{π}{2}}]$,求角x;
(Ⅱ)若$f(x)=\overrightarrow{m•}\overrightarrow n$,求函数f(x)的最小正周期和单调递增区间.
分析 (I)利用向量平行得到$tanx=\frac{{\sqrt{3}}}{3}$或sinx=0,根据x的范围即可求出;
(Ⅱ)利用平面向量的数量积运算法则化简f(x)解析式,再利用两角和与差的正弦函数公式化为一个叫角的正弦函数,找出ω的值,代入周期公式即可求出f(x)的最小正周期;根据正弦函数的递增区间求出x的范围,即为函数f(x)的递增区间.
解答 解:(Ⅰ)∵$\overrightarrow m∥\overrightarrow n$,
∴$\sqrt{3}$sin2x-sinxcosx=0
∴$tanx=\frac{{\sqrt{3}}}{3}$或sinx=0,
∵$x∈[{0,\frac{π}{2}}]$,
∴$x=\frac{π}{6}$或x=0;
(Ⅱ)∵$f(x)=\overrightarrow{m•}\overrightarrow n$=$\sqrt{3}$sinxcosx+sin2x=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x+$\frac{1}{2}$=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$
周期T=$\frac{2π}{2}$=π,
∵2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$$≤\frac{π}{2}$+2kπ,k∈Z,
∴kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,
∴单调递增区间为$[{kπ-\frac{π}{6},kπ+\frac{π}{3}}],k∈Z$.
点评 此题考查了两角和与差的正弦函数公式,平面向量的数量积运算,二倍角的余弦函数公式,正弦函数的单调性,以及三角函数的周期性及其求法,熟练掌握公式是解本题的关键.

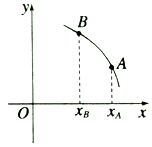
| A. | ${f^'}({x_A})>{f^'}({x_B})$ | B. | ${f^'}({x_A})<{f^'}({x_B})$ | C. | ${f^'}({x_A})={f^'}({x_B})$ | D. | 不能确定 |
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
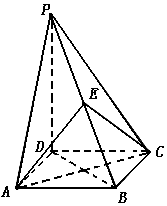 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.