题目内容
15.当x+y+z=1时,则x2+y2+z2的最小值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{27}$ | D. | 3 |
分析 利用条件x+y+z=1,构造柯西不等式(x+y+z)2≤(x2+y2+z2)(12+12+12)进行解题即可.
解答 解:由柯西不等式可知:(x+y+z)2≤(x2+y2+z2)(12+12+12)
故x2+y2+z2≥$\frac{1}{3}$,即:x2+2y2+3z2的最小值为$\frac{1}{3}$.
故选:A.
点评 本题主要考查了函数的最值,以及柯西不等式的应用,解题的关键是利用(x+y+z)2≤(x2+y2+z2)(12+12+12)进行解决.

练习册系列答案
相关题目
5.关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料
试用最小二乘法求出y关于x的线性回归方程
参考公式:
用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
| x | 1 | 2 | 3 | 4 |
| y | 0.5 | 1 | 1.5 | 3 |
参考公式:
用最小二乘法求线性回归方程系数公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
3.已知$\overrightarrow{a}$=(1,0),|$\overrightarrow{b}$|=$\sqrt{2}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
20.若函数f(x)=cos(2x+φ)是奇函数,则φ可取一个值为( )
| A. | -π | B. | -$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
7.已知函数y=f(x)的图象如图,则${f^'}({x_A})与{f^'}({x_B})$的关系是:( )
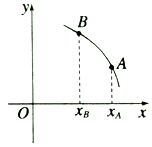

| A. | ${f^'}({x_A})>{f^'}({x_B})$ | B. | ${f^'}({x_A})<{f^'}({x_B})$ | C. | ${f^'}({x_A})={f^'}({x_B})$ | D. | 不能确定 |
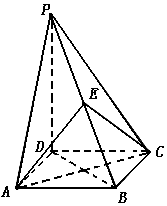 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.