题目内容
17.已知f(α)=$\frac{{sin(π-α)cos(2π-α)sin(-α+\frac{3π}{2})}}{tan(-α-π)sin(-π-α)cos(-π+α)}$;(1)化简f(α);
(2)若α的终边在第二象限,$sinα=\frac{3}{5}$,求f(α)的值.
分析 (1)直接由三角函数的诱导公式化简即可得答案;
(2)由同角三角函数基本关系计算即可得答案.
解答 解:(1)f(α)=$\frac{{sin(π-α)cos(2π-α)sin(-α+\frac{3π}{2})}}{tan(-α-π)sin(-π-α)cos(-π+α)}$
=$\frac{sinα•cosα•(-cosα)}{-tanα•sinα•(-cosα)}=-\frac{co{s}^{2}α}{sinα}$;
(2)∵$sinα=\frac{3}{5}$,
∴$co{s}^{2}α=1-si{n}^{2}α=1-\frac{9}{25}=\frac{16}{25}$.
∴f(α)=$\frac{-co{s}^{2}α}{sinα}=-\frac{16}{15}$.
点评 本题考查了三角函数的诱导公式,考查了同角三角函数基本关系,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知函数y=f(x)的图象如图,则${f^'}({x_A})与{f^'}({x_B})$的关系是:( )
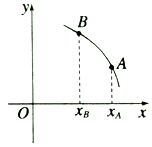

| A. | ${f^'}({x_A})>{f^'}({x_B})$ | B. | ${f^'}({x_A})<{f^'}({x_B})$ | C. | ${f^'}({x_A})={f^'}({x_B})$ | D. | 不能确定 |
6.若函数$f(x)=2sin(ωx+\frac{π}{4})(ω>0)$与$g(x)=2cos(2x-\frac{π}{4})(ω>0)$的对称轴完全相同,则函数$f(x)=2sin(ωx+\frac{π}{4})(ω>0)$在[0,π]上的一个递增区间是( )
| A. | $[0,\frac{π}{8}]$ | B. | $[0,\frac{π}{4}]$ | C. | $[\frac{π}{8},π]$ | D. | $[\frac{π}{4},π]$ |
7.函数$y=tan(\frac{π}{4}-x)$的定义域是( )
| A. | {x|x≠$\frac{π}{4}$,k∈Z x∈R} | B. | {x|x≠kπ$+\frac{π}{4}$,k∈Z,x∈R} | ||
| C. | {x|x≠$-\frac{π}{4}$,k∈Z x∈R} | D. | {x|x≠kπ$+\frac{3}{4}π$,k∈Z,x∈R} |