题目内容
18.在底面半径为2母线长为4的圆锥中内接一个高为x的正四棱柱,(1)用x表示正四棱柱的侧面积;
(2)x为何值时,正四棱柱的侧面积最大?
分析 (1)设四棱柱的底面边长为x,侧棱长为y,可得y=2$\sqrt{3}$-$\frac{\sqrt{6}}{2}$x,由此用x表示正四棱柱的侧面积;
(2)由(1)可得S侧=-2$\sqrt{6}$(x-$\sqrt{2}$)2+4$\sqrt{6}$,结合二次函数的单调性与最值,可得结论.
解答 解:(1)设四棱柱的底面边长为x,侧棱长为y,则有$\frac{\frac{\sqrt{2}}{2}x}{2}=\frac{\sqrt{16-4}-y}{\sqrt{16-4}}$
则y=2$\sqrt{3}$-$\frac{\sqrt{6}}{2}$x,
∴S侧=4x×y=4x(2$\sqrt{3}$-$\frac{\sqrt{6}}{2}$x)(0<x<2$\sqrt{2}$)
(2)S侧=-2$\sqrt{6}$(x-$\sqrt{2}$)2+4$\sqrt{6}$,
则当x=$\sqrt{2}$时,S侧有最大值.
即四棱柱的侧面积最大时,该四棱柱的底面边长为$\sqrt{2}$.
点评 本题考查了利用几何体的轴截面分析量的等量关系,注意不同量的转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知角θ在第二象限,且$|{sin\frac{θ}{2}}|=-sin\frac{θ}{2}$,则 $\frac{θ}{2}$在( )
| A. | 第一象限或第三象限 | B. | 第二象限或第四象限 | ||
| C. | 第三象限 | D. | 第四象限 |
3.已知$\overrightarrow{a}$=(1,0),|$\overrightarrow{b}$|=$\sqrt{2}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
7.已知函数y=f(x)的图象如图,则${f^'}({x_A})与{f^'}({x_B})$的关系是:( )
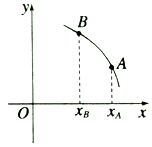

| A. | ${f^'}({x_A})>{f^'}({x_B})$ | B. | ${f^'}({x_A})<{f^'}({x_B})$ | C. | ${f^'}({x_A})={f^'}({x_B})$ | D. | 不能确定 |
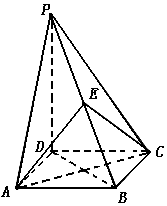 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.