题目内容
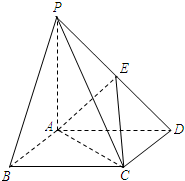 如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.(1)证明PB∥底面ACE;
(2)求直线PB与平面PAC所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)首先利用中位线得到线线平行,进一步转化为线面平行.
(2)首先利用绵绵的垂直转化成线面的垂直,进一步得出线面的夹角,最后利用解直角三角形知识求出结果.
(2)首先利用绵绵的垂直转化成线面的垂直,进一步得出线面的夹角,最后利用解直角三角形知识求出结果.
解答:

证明:(1)连结BD交AC于O,连结EO,
则:EO是△PBD的中位线,
所以:PB∥EO
因为PB?平面ACE,EO?平面ACE
所以:PB∥平面ACE
(2)作BH⊥AC于H,连结PH
因为:PA⊥底面ABCD,
所以:平面PAC⊥平面ABCD
由两平面垂直的性质定理得,BH⊥平面PAC
所以:∠BPH就是直线PB与平面PAC所成的角.
因为 PB=5,BH=
,
所以:sin∠BPH=
=
,
即直线PB与平面PAC所成的角的正弦值为
.

证明:(1)连结BD交AC于O,连结EO,
则:EO是△PBD的中位线,
所以:PB∥EO
因为PB?平面ACE,EO?平面ACE
所以:PB∥平面ACE
(2)作BH⊥AC于H,连结PH
因为:PA⊥底面ABCD,
所以:平面PAC⊥平面ABCD
由两平面垂直的性质定理得,BH⊥平面PAC
所以:∠BPH就是直线PB与平面PAC所成的角.
因为 PB=5,BH=
| 12 |
| 5 |
所以:sin∠BPH=
| BH |
| PB |
| 12 |
| 25 |
即直线PB与平面PAC所成的角的正弦值为
| 12 |
| 25 |
点评:本题考查的知识要点:线面平行的判定定理,线面的夹角,解直角三角形知识,属于基础题型.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
设f(x)=
,h(x)=
,则f(h(e))等于( )
|
|
| A、1 | B、0 | C、-1 | D、e |
“φ=
”是y=cos(x+φ)为奇函数的( )
| π |
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
集合A={(x,y)|
=1},B={(x,y)|3x+y-1=0}全集U={(x,y)|x∈R,y∈R},则(∁UA)∩B=( )
| y+2 |
| x-1 |
| A、{1,-2} |
| B、{(1,-2)} |
| C、{(-1,2)} |
| D、{(x,y)|3x+y-1=0} |

 在三棱锥P-ABC中,平面PBC⊥平面ABC,AB=AC,E,F分别为BC,BP的中点,求证:(1)直线EF∥平面PAC;
在三棱锥P-ABC中,平面PBC⊥平面ABC,AB=AC,E,F分别为BC,BP的中点,求证:(1)直线EF∥平面PAC;