题目内容
已知不等式ax2>3x-2的解集为{x|x<1或x>b}.
(1)求a,b;
(2)解不等式acx2-(ac+b)x+b<0.
(1)求a,b;
(2)解不等式acx2-(ac+b)x+b<0.
考点:一元二次不等式的解法
专题:分类讨论,不等式的解法及应用
分析:(1)由一元二次不等式与对应方程的实数集之间的关系,结合根与系数的关系,求出a、b的值;
(2)由(1)的结论,化简不等式acx2-(ac+b)x+b<0,讨论c的取值,解含有字母系数的不等式即可.
(2)由(1)的结论,化简不等式acx2-(ac+b)x+b<0,讨论c的取值,解含有字母系数的不等式即可.
解答:
解:(1)∵不等式ax2>3x-2的解集为{x|x<1或x>b},
∴x1=1与x2=b是方程ax2-3x+2=0的两个实数根,且b>1,
由根与系数的关系,得
;
解得a=1,b=2;
(2)由(1)知,不等式acx2-(ac+b)x+b<0可化为不等式cx2-(c+2)x+2<0,
即(cx-2)(x-1)<0;
①当c=0时,不等式为x-1>0,解集为{x|x>1};
②当c>0时,不等式为(x-
)(x-1)<0,
(i)c=2时,解集为Φ,
(ii)c>2时,
<1,此时解集为{x|
<x<1},
(iii)0<c<2时,
>1,此时解集为{x|1<x<
};
③当c<0时,不等式为(x-
)(x-1)>0,此时不等式解集为{x|x>1,或x<
};
综上,c<0时,解集为{x|x>1,或x<
},
c=0时,解集为{x|x>1},
0<c<2时,解集为{x|1<x<
},
c=2时,解集为Φ,
c>2时,解集为{x|
<x<1}.
∴x1=1与x2=b是方程ax2-3x+2=0的两个实数根,且b>1,
由根与系数的关系,得
|
解得a=1,b=2;
(2)由(1)知,不等式acx2-(ac+b)x+b<0可化为不等式cx2-(c+2)x+2<0,
即(cx-2)(x-1)<0;
①当c=0时,不等式为x-1>0,解集为{x|x>1};
②当c>0时,不等式为(x-
| 2 |
| c |
(i)c=2时,解集为Φ,
(ii)c>2时,
| 2 |
| c |
| 2 |
| c |
(iii)0<c<2时,
| 2 |
| c |
| 2 |
| c |
③当c<0时,不等式为(x-
| 2 |
| c |
| 2 |
| c |
综上,c<0时,解集为{x|x>1,或x<
| 2 |
| c |
c=0时,解集为{x|x>1},
0<c<2时,解集为{x|1<x<
| 2 |
| c |
c=2时,解集为Φ,
c>2时,解集为{x|
| 2 |
| c |
点评:本题考查了一元二次不等式与对应的方程解的关系,考查了根与系数的关系的应用问题,也考查了含有字母系数的不等式的解法与应用问题,是基础题.

练习册系列答案
相关题目
函数f(x)=|x+2|的单调递减区间是( )
| A、(-∞,-2] |
| B、(-∞,2] |
| C、(-∞,0] |
| D、无减区间 |
递增等差数列{an}中,若a1+a9=0,则Sn取最小值时n等于( )
| A、4 | B、5 | C、6 | D、4或5 |
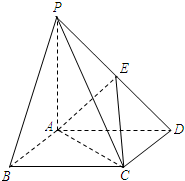 如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.