题目内容
从甲城市到乙城市m分钟的电话费由函数f（m）=1.06×（
[m]+
）给出，其中m＞0，[m]表示不大于m的最大整数（如[3]=3，[3.9]=3，[3.1]=3），则从甲城市到乙城市7.8分钟的电话费为 ．
| 3 |
| 4 |
| 7 |
| 4 |
考点：函数的值
专题：函数的性质及应用
分析：由条件根据新定义求得从甲城市到乙城市7.8分钟的电话费f（7.8）的值．
解答：
解：由题意可得，从甲城市到乙城市7.8分钟的电话费为 f（7.8）=1.06×（
[7.8]+
）=1.06×（
×7+
）=7.42，
故答案为：7.42．
| 3 |
| 4 |
| 7 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
故答案为：7.42．
点评：本题主要考查新定义、求函数的值，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
执行如图所示的程序框图，若p=0.8，则输出的n=（ ）
| A、5 | B、2 | C、3 | D、4 |
设a=40.2，b=0.24，c=log40.2，则a，b，c的大小关系为（ ）
| A、a＞b＞c |
| B、b＞c＞a |
| C、c＞a＞b |
| D、b＞a＞c |
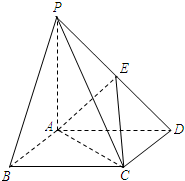如图，四棱锥P-ABCD中，PA⊥底面ABCD，ABCD是矩形，E是棱PD的中点，PA=AD=4，AB=3．不等式组
所确定的平面区域记为D，当M（x，y）∈D时，A（-2，0），B（2，0），则
•
的最小值为（ ）
|
| AM |
| BM |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|