题目内容
正数x、y满足
+
=3,则xy的最小值为 .
| 2 |
| x |
| 1 |
| y |
考点:基本不等式
专题:不等式的解法及应用
分析:本题可以直接利用基本不等式求出xy的最小值,得到本题结论.
解答:
解:∵正数x、y满足
+
=3,
∴3=
+
≥2
,
即
≥
,
xy≥
.
当且仅当
=
,即x=
,y=
时取等号.
故答案为:
.
| 2 |
| x |
| 1 |
| y |
∴3=
| 2 |
| x |
| 1 |
| y |
|
即
| xy |
2
| ||
| 3 |
xy≥
| 8 |
| 9 |
当且仅当
| 2 |
| x |
| 1 |
| y |
| 4 |
| 3 |
| 2 |
| 3 |
故答案为:
| 8 |
| 9 |
点评:本题考查了基本不等式,本题难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
设方程sin4x=0的解集为M,方程cos2x=1的解集为P,则M与P之间的关系是( )
| A、P?M | B、M?P |
| C、M=P | D、M∩P=∅ |
函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A)有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t度低调函数.已知定义域为[0,+∞)的函数f(x)=-|mx-3|,且f(x)为[0,+∞)上的6度低调函数,那么实数m的取值范围是( )
| A、[0,1] |
| B、[1,+∞) |
| C、(-∞,0) |
| D、(-∞,0]∪[1,+∞) |
在△ABC中,D为边BC的中点,则下列向量关系式正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
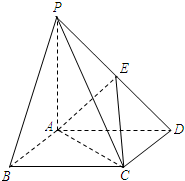 如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.