题目内容
 在三棱锥P-ABC中,平面PBC⊥平面ABC,AB=AC,E,F分别为BC,BP的中点,求证:(1)直线EF∥平面PAC;
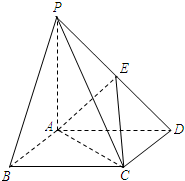
在三棱锥P-ABC中,平面PBC⊥平面ABC,AB=AC,E,F分别为BC,BP的中点,求证:(1)直线EF∥平面PAC;(2)平面AEF⊥平面PBC.
考点:直线与平面垂直的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)利用E,F分别是BC,BP的中点,说明EF∥PC,通过直线与平面平行的判定定理直接证明EF∥平面PAC.
(2)证明AE⊥BC,利用平面与平面垂直的判定定理证明AE⊥平面ABC,再通过面面垂直的判定定理证明平面AEF⊥平面PBC.
(2)证明AE⊥BC,利用平面与平面垂直的判定定理证明AE⊥平面ABC,再通过面面垂直的判定定理证明平面AEF⊥平面PBC.
解答:
证明:(1)∵E,F分别是BC,BP的中点,∴EF∥PC.
又EF?平面PAC,
PC?平面PAC,
∴EF∥平面PAC.
(2)在△ABC中,∵AB=AC,E为BC中点,
∴AE⊥BC.
∵平面PBC⊥平面ABC,
平面PBC∩平面ABC=BC,
∴AE⊥平面PBC.
又AE?平面ABC,
∴平面AEF⊥平面PBC.
又EF?平面PAC,
PC?平面PAC,
∴EF∥平面PAC.
(2)在△ABC中,∵AB=AC,E为BC中点,
∴AE⊥BC.
∵平面PBC⊥平面ABC,
平面PBC∩平面ABC=BC,
∴AE⊥平面PBC.
又AE?平面ABC,
∴平面AEF⊥平面PBC.
点评:本题考查直线与平面平行的判定定理,平面与平面垂直的性质定理,考查空间想象能力,逻辑推理能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
递增等差数列{an}中,若a1+a9=0,则Sn取最小值时n等于( )
| A、4 | B、5 | C、6 | D、4或5 |
设a=40.2,b=0.24,c=log40.2,则a,b,c的大小关系为( )
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、b>a>c |
不等式组
所确定的平面区域记为D,当M(x,y)∈D时,A(-2,0),B(2,0),则
•
的最小值为( )
|
| AM |
| BM |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设方程sin4x=0的解集为M,方程cos2x=1的解集为P,则M与P之间的关系是( )
| A、P?M | B、M?P |
| C、M=P | D、M∩P=∅ |
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.