题目内容
集合A={(x,y)|
=1},B={(x,y)|3x+y-1=0}全集U={(x,y)|x∈R,y∈R},则(∁UA)∩B=( )
| y+2 |
| x-1 |
| A、{1,-2} |
| B、{(1,-2)} |
| C、{(-1,2)} |
| D、{(x,y)|3x+y-1=0} |
考点:交、并、补集的混合运算
专题:集合
分析:由补集的运算和集合A求出∁UA,再由交集的运算和直线的方程求出(∁UA)∩B.
解答:
解:由
=1得,y=x-3(且x≠1、y≠-2),
因为全集U={(x,y)|x∈R,y∈R},
所以∁UA={(x,y)|y≠x-3或x=1、y=-2},
又
得,
,
所以(∁UA)∩B={(x,y)|3x+y-1=0},
故选:D.
| y+2 |
| x-1 |
因为全集U={(x,y)|x∈R,y∈R},
所以∁UA={(x,y)|y≠x-3或x=1、y=-2},
又
|
|
所以(∁UA)∩B={(x,y)|3x+y-1=0},
故选:D.
点评:本题考查了交、并、补集的混合运算,以及点集的运算,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知点P是△ABC的内心(三个内角平分线交点)、外心(三条边的中垂线交点)、重心(三条中线交点)、垂心(三个高的交点)之一,且满足2
•
=
2-
2
,则点P一定是△ABC的( )
| AP |
| BC |
| AC |
| AB |
,则点P一定是△ABC的( )
| A、内心 | B、外心 | C、重心 | D、垂心 |
函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A)有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t度低调函数.已知定义域为[0,+∞)的函数f(x)=-|mx-3|,且f(x)为[0,+∞)上的6度低调函数,那么实数m的取值范围是( )
| A、[0,1] |
| B、[1,+∞) |
| C、(-∞,0) |
| D、(-∞,0]∪[1,+∞) |
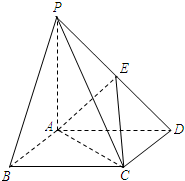 如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.