题目内容
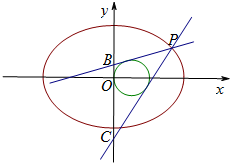 设椭圆E:
设椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)点P是椭圆E上横坐标大于2的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于△PBC,试判断点P在何位置时△PBC的面积S最小,并证明你的判断.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由已知条件推导出a=
b,
=
,由此能求出椭圆方程.
( II)设P(x0,y0)(2<x0≤2
),B(0,m),C(0,n).不妨设m>n,由已知条件推导出m,n是方程(x0-2)x2+2y0x-x0=0的两个根,由此能求出点P的横坐标为x0=2
时,△PBC的面积S最小.
| 2 |
| b2 |
| a |
| 3 |
( II)设P(x0,y0)(2<x0≤2
| 3 |
| 3 |
解答:
解:( I)由已知a=
b,
=
,…(2分)
解得:a=2
,b=
,
故所求椭圆方程为
+
=1.…(4分)
( II)设P(x0,y0)(2<x0≤2
),
B(0,m),C(0,n).不妨设m>n,
则直线PB的方程为lPB:y-m=
x,…(5分)
即(y0-m)x-x0y+x0m=0,
又圆心(1,0)到直线PB的距离为1,
即
=1,x0>2,
化简得(x0-2)m2+2y0m-x0=0,…(7分)
同理,(x0-2)n2+2y0n-x0=0,
∴m,n是方程(x0-2)x2+2y0x-x0=0的两个根,
∴m+n=
,mn=
,
则(m-n)2=
,…(9分)
∵P(x0,y0)是椭圆上的点,
∴
=6(1-
),∴(m-n)2=
.
则S2=
•
•
=
•
=
•
,
令x0-2=t(0<t≤2(
-1)),
则x0=t+2,令f(t)=
,
化简,得f(t)=
t2+2t+6+
+
,
则f′(t)=t+2-
-
=
,
令f'(t)=0,得t=2
,而2(
-1)<2
,
∴函数f(t)在[0,2(
-1)]上单调递减,
当t=2(
-1)时,f(t)取到最小值,
此时x0=2
,
即点P的横坐标为x0=2
时,△PBC的面积S最小.…(12分)
| 2 |
| b2 |
| a |
| 3 |

解得:a=2
| 3 |
| 6 |
故所求椭圆方程为
| x2 |
| 12 |
| y2 |
| 6 |
( II)设P(x0,y0)(2<x0≤2
| 3 |
B(0,m),C(0,n).不妨设m>n,
则直线PB的方程为lPB:y-m=
| y0-m |
| x0 |
即(y0-m)x-x0y+x0m=0,
又圆心(1,0)到直线PB的距离为1,
即
| |y0-m+x0m| | ||
|
化简得(x0-2)m2+2y0m-x0=0,…(7分)
同理,(x0-2)n2+2y0n-x0=0,
∴m,n是方程(x0-2)x2+2y0x-x0=0的两个根,
∴m+n=
| -2y0 |
| x0-2 |
| -x0 |
| x0-2 |
则(m-n)2=
4
| ||||
| (x0-2)2 |
∵P(x0,y0)是椭圆上的点,
∴
| y | 2 0 |
| ||
| 12 |
2
| ||
| (x0-2)2 |
则S2=
| 1 |
| 4 |
2
| ||
| (x0-2)2 |
| x | 2 0 |
| ||
| 2(x0-2)2 |
| x | 2 0 |
| (x0-2)2+8 |
| 2(x0-2)2 |
| x | 2 0 |
令x0-2=t(0<t≤2(
| 3 |
则x0=t+2,令f(t)=
| (t2+8)(t+2)2 |
| 2t2 |
化简,得f(t)=
| 1 |
| 2 |
| 16 |
| t |
| 16 |
| t2 |
则f′(t)=t+2-
| 16 |
| t2 |
| 32 |
| t3 |
| (t+2)(t3-16) |
| t3 |
令f'(t)=0,得t=2
| 3 | 2 |
| 3 |
| 3 | 2 |
∴函数f(t)在[0,2(
| 3 |
当t=2(
| 3 |
此时x0=2
| 3 |
即点P的横坐标为x0=2
| 3 |
点评:本题考查椭圆方程的求法,考查点在何处时三角形面积最小的判断和证明,解题时要认真审题,注意函数的单调性的合理运用.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
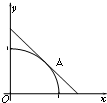 如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的最大值为( )
如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的最大值为( )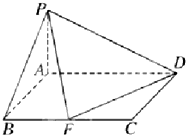 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,F为线段BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,F为线段BC的中点.