题目内容

设点P是函数f（x）=sinωx的图象C的一个对称中心，若点P到图象C的对称轴的最小值是
π
8
，则f（x）的最小正周期是
 
．
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由题意可得最小正周期T=
2π
ω
=4×
π
8
，求得ω=4的值，可得f（x）的最小正周期．
解答： 解：由题意可得最小正周期T=
2π
ω
=4×
π
8
，
∴ω=4，
∴f（x）的最小正周期是
2π
 4
=
π
2
，
故答案为：
π
2
．
点评：本题主要考查函数y=Asin（ωx+φ）的图象和性质，属于基础题
练习册系列答案
相关题目
设同时满足以下两个条件的有穷数列a1，a2，a3，…，an为n（n=2，3，4，…）阶“期待数列”：
①a1+a2+a3+…+an=0；
②|a1|+|a2|+|a3|+…+|an|=1．
（Ⅰ）若等比数列{an}为2k（k∈N*）阶“期待数列”，求公比q；
（Ⅱ）记n阶“期待数列”{ai}的前k项和为Sk（k=1，2，3，…，n）．
（1）求证：|Sk|≤
1
2
；
（2）若存在m∈{1，2，3，…，n}，使得Sm=
1
2
．试问：数列{Si}（i=1，2，3，…，n）能否为n阶“期待数列”？若能，求出所有这样的数列；否则，请说明理由．
点M（x，y）是不等式组
0≤x≤
3
y≤3
x≤
3
y
表示的平面区域Ω内的一动点，且不等式2x-y+m≥0总成立，则m的取值范围是
 
．
已知函数f（x）=2sin（ωx+φ）（其中x∈R，ω＞0，-π＜φ＜π）的部分图象如图所示，则函数f（x）的解析式是
 
．
①已知钝二面角α-l-β的大小为θ，
u
，
v
分别是平面α，β的法向量则cosθ=-|cos（
u
，
v
）|，
②圆x2+（y+1）2=3绕直线kx-y-1=0旋转一周所得几何体的体积是4π，
③圆锥底面半径为
3
，母线长为2，则过圆锥顶点的截面面积的最大值为
3

④已知A，B，C，D四点共面，
OA
=an
OB
-an-1
OC
-
OD
，又数列{an}中，a1=-11，则数列{an}的前n项和Sn有最小值-36．
正确的是
 
．
定义在R上的函数f（x）过点（0，1），且f′（x）=2x，则
∫
1
0
f（x）dx的值等于
 
．
正三角形ABC的边长为2
3
，将它沿高AD翻折，使点B与点C间的距离为
3
，此时四面体ABCD的外接球的体积为
 
．
已知x，y的取值如下表，从所得的散点图分析，y与x线性相关，则
y
=1.1x+
a
，则
a
=（　　）
x 0 1 3 4
y 1 2 3 6
A、-0.4B、0.8
C、-1D、-1.2
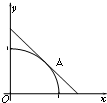如图，设圆弧x2+y2=1（x≥0，y≥0）与两坐标轴正半轴围成的扇形区域为M，过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N．现随机在区域N内投一点B，若设点B落在区域M内的概率为P，则P的最大值为（　　）
A、
1
4
B、
π
8
C、
1
2
D、
π
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网