题目内容
已知函数 f（x）=ax3+f′（2）x2+3，若 f′（1）=-5，则f′（2）=（ ）
| A、-l | B、-2 | C、-3 | D、-4 |
考点：导数的运算
专题：导数的概念及应用
分析：根据函数的导数公式，求函数的导数，即可得到结论．
解答：
解：∵f（x）=ax3+f′（2）x2+3，
∴f′（x）=3ax2+2xf′（2），
令x=2，则f′（2）=12a+4f′（2），
即f′（2）=-4a，
即f′（x）=3ax2-8ax，
∵f′（1）=-5，
∴f′（1）=-5=3a-8a=-5a，
解得a=1，
即f′（x）=3x2-8x，
则f′（2）=12-16=-4，
故选：D．
∴f′（x）=3ax2+2xf′（2），
令x=2，则f′（2）=12a+4f′（2），
即f′（2）=-4a，
即f′（x）=3ax2-8ax，
∵f′（1）=-5，
∴f′（1）=-5=3a-8a=-5a，
解得a=1，
即f′（x）=3x2-8x，
则f′（2）=12-16=-4，
故选：D．
点评：本题主要考查函数的导数计算，根据条件求出a和f′（1）是解决本题的根据．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
复数
的虚部是（ ）
| i2014 |
| 1-2i |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
二项式（x-1）n的奇数项二项式系数和64，若（x-1）n=a0+a1（x+1）+a2（x+1）2+…+an（x+1）n，则a1等于（ ）
| A、-14 | B、448 |
| C、-1024 | D、-16 |
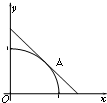如图，设圆弧x2+y2=1（x≥0，y≥0）与两坐标轴正半轴围成的扇形区域为M，过圆弧上一点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N．现随机在区域N内投一点B，若设点B落在区域M内的概率为P，则P的最大值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知复数z1=1-i，z2=1+i，则
等于（ ）
| z1•z2 |
| i |
| A、2i | B、-2i |
| C、2+i | D、-2+i |
如图，在山脚A测得山顶P的仰角为30°，沿倾斜角为15°的斜坡向上走a米到B，在B处测得山顶P的仰角为60°，求山高h=（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、a |