题目内容
设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则x•f(x)>0的解集是( )
| A、{x|-3<x<0,或x>3} |
| B、{x|x<-3,或0<x<3} |
| C、{x|x<-3,或x>3} |
| D、{x|-3<x<0,或0<x<3} |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:先由函数性质得出函数f(x)在(-∞,0)内是增函数,且f(3)=0,然后分析f(x)符号,解不等式.
解答:
解:∵f(x)是R上的奇函数,且在(0,+∞)内是增函数,
∴f(x)在(-∞,0)内是增函数,
又∵f(-3)=0,
∴f(3)=0,
∴当x∈(-∞,-3)∪(0,3)时,f(x)<0;
当x∈(-3,0)∪(3,+∞)时,f(x)>0;
∴x•f(x)>0的解集是(-∞,-C3)∪(3,+∞)
故选:C.
∴f(x)在(-∞,0)内是增函数,
又∵f(-3)=0,
∴f(3)=0,
∴当x∈(-∞,-3)∪(0,3)时,f(x)<0;
当x∈(-3,0)∪(3,+∞)时,f(x)>0;
∴x•f(x)>0的解集是(-∞,-C3)∪(3,+∞)
故选:C.
点评:本题考查函数性质,主要是单调性和奇偶性,利用函数性质求解不等式.

练习册系列答案
相关题目
已知集合A={x|1<x<3},B={x|x≤2},则集合A∩B( )
| A、(0,1) |
| B、(0,2] |
| C、(1,2) |
| D、(1,2] |
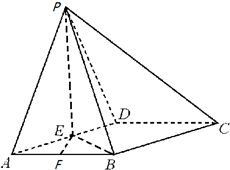 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E,F分别为AD,AB的中点,PE⊥平面ABCD,BE⊥平面PAD.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E,F分别为AD,AB的中点,PE⊥平面ABCD,BE⊥平面PAD. 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=