题目内容
11.若f(x)=x3+ax2+bx-a2-7a在x=1处取得极大值10,则$\frac{b}{a}$的值为$-\frac{3}{2}$.分析 求出导函数,根据极值的定义得出f(1)=10,f'(1)=0,且f'(x)=0有实数解,进而得出a,b的值.
解答 解:f(x)=x3+ax2+bx-a2-7a,
f'(x)=3x2+2ax+b,
∵在x=1处取得极大值10,
∴f(1)=10,f'(1)=0,且f'(x)=0有实数解,
∴a=-2(舍去),a=-6,
∴b=1,
∴$\frac{b}{a}$=$-\frac{3}{2}$.
故答案为$-\frac{3}{2}$.
点评 本题考查了极值的概念,属于基础题型,应熟练掌握.

练习册系列答案
相关题目
19.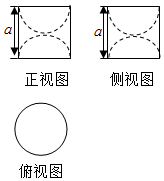 某几何体的三视图如图所示,若该几何体的体积为$\frac{2π}{3}$,则a的值为( )
某几何体的三视图如图所示,若该几何体的体积为$\frac{2π}{3}$,则a的值为( )
 某几何体的三视图如图所示,若该几何体的体积为$\frac{2π}{3}$,则a的值为( )
某几何体的三视图如图所示,若该几何体的体积为$\frac{2π}{3}$,则a的值为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\root{3}{2}$ |
6.已知a∈R,直线l:x+ay+a-2=0,圆M:(x-1)2+(y-1)2=1,则“a=0”是“直线l与圆M相切”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
20.已知函数f(x)=ax+xlnx图象在点(e,f(e))(e为自然对数的底数)处的切线斜率为3.
(1)求实数a的值;
(2)若k∈Z,且f(x)-k(x-1)>0对任意x>1恒成立,求k的最大值.
(1)求实数a的值;
(2)若k∈Z,且f(x)-k(x-1)>0对任意x>1恒成立,求k的最大值.
1.等差数列{an}中a1=1,a5-a2=6,则a6的值为( )
| A. | 5 | B. | 11 | C. | 13 | D. | 15 |