题目内容
20．已知函数f（x）=ax+xlnx图象在点（e，f（e））（e为自然对数的底数）处的切线斜率为3．（1）求实数a的值；
（2）若k∈Z，且f（x）-k（x-1）＞0对任意x＞1恒成立，求k的最大值．
分析 （1）求出函数的导数，计算f′（e）=3，求出a的值即可；
（2）问题等价于k＜$\frac{x+xlnx}{x-1}$对任意x＞1恒成立，令g（x）=$\frac{x+xlnx}{x-1}$，根据函数的单调性求出k的最大值即可．
解答 解：（1）由已知得f′（x）=a+lnx+1，故f′（e）=3，
∴a+lne+1=3，∴a=1；…（5分）
（2）由（1）知，f（x）=x+xlnx，
等价于k＜$\frac{x+xlnx}{x-1}$对任意x＞1恒成立，
令g（x）=$\frac{x+xlnx}{x-1}$，则g′（x）=$\frac{x-lnx-2}{{（x-1）}^{2}}$，
令h（x）=x-lnx-2，x＞1，
则h′（x）=1-$\frac{1}{x}$=$\frac{x-1}{x}$＞0，
∴h（x）在（1，+∞）上单调增加，
∵h（3）=1-ln3＜0，h（4）=2-2ln2＞0，
∴h（x）在（1，+∞）上在唯一实数根x0，满足x0∈（3，4），且h（x0）=0
当x∈（1，x0）时，h（x）＜0，∴g′（x）＜0；
当x∈（x0，+∞）时，h（x）＞0，∴g′（x）＞0，
∴g（x）在（1，x0）上单调递减，在（x0，+∞）上单调递增，
∴g（x）min=g（x0）=$\frac{{x}_{0}（1{+x}_{0}-2）}{{x}_{0}-1}$=x0∈（3，4），
∴k＜g（x）min=x0∈（3，4），
∴整数k的最大值为3．…（12分）
点评 本题考查了函数的单调性、最值问题，考查导数的应用以及转化思想，是一道中档题．
练习册系列答案
天天向上一本好卷系列答案
相关题目
10．执行如图所示的程序框图，输出的S值为（ ）
| A． | 4 | B． | 8 | C． | 14 | D． | 18 |
8．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F，直线y=kx（k＞0）与椭圆C交于A，B两点，若$AF⊥BF，∠FAB∈（0，\frac{π}{12}]$，则C的离心率取值范围为（ ）
| A． | $[\frac{{\sqrt{2}}}{2}，1）$ | B． | $[\frac{{\sqrt{6}}}{3}，1）$ | C． | $[\frac{{\sqrt{3}}}{3}，1）$ | D． | $[\frac{2}{3}，1）$ |
15．已知${log_{\frac{1}{2}}}a＜{log_{\frac{1}{2}}}b$，则下列不等式一定成立的是（ ）
| A． | ${（{\frac{1}{4}}）^a}＜{（{\frac{1}{3}}）^b}$ | B． | $\frac{1}{a}＞\frac{1}{b}$ | C． | ln（a-b）＞0 | D． | 3a-b＜1 |
5．已知离心率为e的双曲线$\frac{x^2}{a^2}-\frac{y^2}{7}=1$，其与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点重合，则e的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4\sqrt{23}}{23}$ | C． | $\frac{4}{3}$ | D． | $\frac{\sqrt{23}}{4}$ |
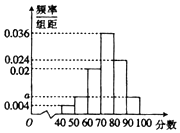某高校在举行艺术类高考招生考试时，对100个考生进行了一项专业水平考试，考试成绩满分为100分，成绩出来后，老师对每个成绩段[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]的人数进行了统计，丙得到如图所示的频率分布直方图．