题目内容
| ∫ |
| 2 |
| 1+x2 |
| 1 | ||
4
|
考点：微积分基本定理
专题：导数的综合应用
分析：由不定积分可得
cosxdx=sinx+C，
（-
）dx=arccotx+C，
dx=
arcsinx+C，代入
（cosx-
+
）dx=
cosxdx+
（-
）dx+
dx，计算可得．
| ∫ |
| ∫ |
| 2 |
| 1+x2 |
| ∫ |
| 1 | ||
4
|
| 1 |
| 4 |
| ∫ |
| 2 |
| 1+x2 |
| 1 | ||
4
|
| ∫ |
| ∫ |
| 2 |
| 1+x2 |
| ∫ |
| 1 | ||
4
|
解答：
解：∵
cosxdx=sinx+C，
（-
）dx=arccotx+C，
dx=
arcsinx+C
∴
（cosx-
+
）dx
=
cosxdx+
（-
）dx+
dx
=sinx+arccotx+
arcsinx+C
故答案为：sinx+arccotx+
arcsinx+C，（C为常数）
| ∫ |
| ∫ |
| 2 |
| 1+x2 |
| ∫ |
| 1 | ||
4
|
| 1 |
| 4 |
∴
| ∫ |
| 2 |
| 1+x2 |
| 1 | ||
4
|
=
| ∫ |
| ∫ |
| 2 |
| 1+x2 |
| ∫ |
| 1 | ||
4
|
=sinx+arccotx+
| 1 |
| 4 |
故答案为：sinx+arccotx+
| 1 |
| 4 |
点评：本题考查不定积分的求解，属基础题．
练习册系列答案
相关题目
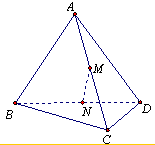已知空间四边形ABCD中，AB⊥CD，AB=4，CD=4
经调查发现，人们长期食用含高浓度甲基汞的鱼类会引起汞中毒，其中罗非鱼体内汞含量比其他鱼偏高．《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm，现从一批数量很大的罗非鱼中随机地抽出15条作为样本，经检测得各条鱼的汞含量的茎叶图（以小数点前的数字为茎，小数点后第一位数字为叶）如图所示