题目内容
5.f(x)=|x+a|+|x-a2|,a∈(-1,3)(1)若a=1,解不等式f(x)≥4
(2)若对?x∈R,?a∈(-1,3),使得不等式m<f(x)成立,求m的取值范围.
分析 (1)若a=1,不等式f(x)≥4为|x+1|+|x-1|≥4,分类讨论解不等式f(x)≥4
(2)对?x∈R,?a∈(-1,3),使得不等式m<f(x)成立,?a∈(-1,3),m<|a+a2|,即可得出m的取值范围.
解答 解:(1)a=1,不等式f(x)≥4为|x+1|+|x-1|≥4
x<-1,不等式化为1-x-x-1≥4,解得x≤-2,∴x≤-2;
-1≤x≤1,不等式化为1-x+x+1≥4,无解;
x>1,不等式化为x-1+x+1≥4,解得x≥2,∴x≥2,
∴不等式的解集为{x|x≤-2或x≥2};
(2)∵f(x)=|x+a|+|x-a2|≥|x+a-x+a2|=|a+a2|
对?x∈R,?a∈(-1,3),使得不等式m<f(x)成立
∴?a∈(-1,3),m<|a+a2|
令g(a)=a+a2,a∈(-1,3),则|g(a)|∈[0,12)
∴m<12.
点评 本题考查不等式的解法,考查恒成立问题,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
13.设集合A={x|$\frac{2}{x-1}$≥1},B={y|y=log2x,0<x≤4},则A∩B=( )
| A. | ∅ | B. | (1,2] | C. | (-∞,1) | D. | [2,3] |
17.一组统计数据x1,x2,x3,x4,x5与另一组统计数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3相比较( )
| A. | 标准差相同 | B. | 中位数相同 | C. | 平均数相同 | D. | 以上都不相同 |
14.已知双曲线Γ:$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1({a>0,b>0})$的上焦点为F1(0,c)(c>0),下焦点为F2(0,-c)(c>0),过点F1作圆x2+y2-$\frac{2c}{3}y+\frac{a^2}{9}$=0的切线与圆相切于点D,与双曲线下支交于点M,若MF2⊥MF1,则双曲线Γ的渐进线方程为( )
| A. | 4x±y=0 | B. | x±4y=0 | C. | 2x±y=0 | D. | x±2y=0 |
15.执行如图所示的程序框图,若输入三个数a=log36,b=log510,c=log714,则输出的结果为( )
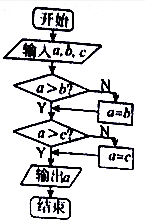

| A. | log36 | B. | log510 | C. | log714 | D. | log26 |