题目内容
15.已知△ABC,AB=$\sqrt{2},AC=4,∠BAC={45°}$,则△ABC外接圆的直径为2$\sqrt{5}$.分析 由已知利用余弦定理可求BC,进而利用正弦定理可求三角形外接圆的半径,进而得解直径的值.
解答 解:∵AB=$\sqrt{2},AC=4,∠BAC={45°}$,
∴由余弦定理可得:BC=$\sqrt{A{C}^{2}+A{B}^{2}-2AB•AC•cos∠BAC}$=$\sqrt{2+16-2×\sqrt{2}×4×\frac{\sqrt{2}}{2}}$=$\sqrt{10}$,
∵设△ABC外接圆的半径为R,由正弦定理可得:R=$\frac{BC}{2sin∠BAC}$=$\frac{\sqrt{10}}{2×\frac{\sqrt{2}}{2}}$=$\sqrt{5}$,
∴△ABC外接圆的直径为2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题主要考查了余弦定理,正弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
3.已知全集U=R,集合A={x|ex>1},B={x|x-3>0},则A∩B=( )
| A. | {x|x<3} | B. | {x|x>0} | C. | {x|1<x<3} | D. | {x|0<x<3} |
10.若x,y满足约束条件$\left\{\begin{array}{l}{-1≤x-y≤1}\\{2≤x+2y≤3}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.市政府为调查市民对本市某项调控措施的态度,随机抽取了500名市民,统计了他们的月收入频率分布和对该项措施的赞成人数,统计结果如表所示:
(1)从月收入在[60,70)的20人中随机抽取3人,求3人中至少2人对对该措施持赞成态度的概率;
(2)根据用样本估计总体的思想,以样本中事件发生的频率作为相应事件发生的概率,在本市随机采访3人,用X表示3人中对该项措施持赞成态度的人数,求X的分布列和数学期望.
| 月收入(单位:百元) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 25 | 100 | 150 | 155 | 50 | 20 |
| 赞成人数 | 10 | 70 | 120 | 150 | 35 | 15 |
(2)根据用样本估计总体的思想,以样本中事件发生的频率作为相应事件发生的概率,在本市随机采访3人,用X表示3人中对该项措施持赞成态度的人数,求X的分布列和数学期望.
4.已知数列{an}为等差数列,其前n项和为Sn,2a7-a8=5,则S11为( )
| A. | 110 | B. | 55 | C. | 50 | D. | 不能确定 |
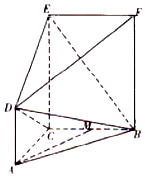 在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.
在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.