题目内容

5．等差数列{an}的前n项和为Sn，若S2=2，S4=8，则S6等于18．

分析 由等差数列{an}的前n项和性质可得：S2，S4-S2，S6-S4成等差数列．即可得出．

解答 解：由等差数列{an}的前n项和性质可得：S2，S4-S2，S6-S4成等差数列．
∴2×6=2+S6-8，解得S6=18．
故答案为：18．

点评 本题考查了等差数列的通项公式与求和公式及其性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
15．公差不为0的等差数列{an}的部分项${a}_{{k}_{1}}$，${a}_{{k}_{2}}$，${a}_{{k}_{3}}$，…构成等比数列{${a}_{{k}_{n}}$}，且k1=1，k2=2，k3=6，则k5为（　　）
A．86B．88C．90D．92
16．已知集合A={y|y=$\frac{4{-e}^{x}}{2}$，x∈R}，B={x|y=lg（1-2x）}
（1）求出集合A，集合B；
（2）求（∁UB）∩A．
13．已知f（x）=x2-（m+$\frac{1}{m}$）x+1
（1）当m=2时，解不等式f（x）≤0
（2）若m＞0，解关于x的不等式f（x）≥0．
20．已知向量$\overrightarrow a$=（{cosx，-$\sqrt{3}$cosx），$\overrightarrow b$=（cosx，sinx），函数f（x）=$\overrightarrow a$•$\overrightarrow b$+1．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若f（θ）=$\frac{5}{6}$，$θ∈（\frac{π}{3}，\frac{2π}{3}），求sin2θ$的值．
10．高二（7）班参加冬令营的6位同学排成一排照相，甲乙必须相邻且甲、乙、丙必须从左到右的排法种数为（　　）
A．120B．60C．36D．72
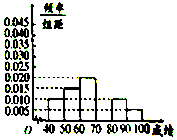17．如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩（均为整数）的频率分布直方图，该直方图恰好缺少了成绩在区间[70，80）内的图形，根据图形的信息，回答下列问题：
（1）求成绩在区间[70，80）内的频率，并补全这个频率分布直方图，并估计这次考试的及格率（60分及以上为及格）；
（2）从成绩在[80，100]内的学生中选出三人，记在90分以上（含90分）的人数为X，求X的分布列及数学期望．
14．在△ABC中，已知a=2，b=2$\sqrt{3}$，B=120°，解此三角形．
15．设函数f（x）是定义在R上的偶函数，f′（x）为其导函数．当x＞0时，xf′（x）+f（x）＞0，且f（1）=0，则不等式f（x）＞0的解集为（　　）
A．（-1，0）∪（0，1）B．（-1，0）∪（1，+∞）C．（-∞，-1）∪（1，+∞）D．（-∞，-1）∪（0，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网