题目内容
15.设函数f(x)是定义在R上的偶函数,f′(x)为其导函数.当x>0时,xf′(x)+f(x)>0,且f(1)=0,则不等式f(x)>0的解集为( )| A. | (-1,0)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
分析 由题意构造函数g(x)=xf (x),再由导函数的符号判断出函数g(x)的单调性,由函数f(x)的奇偶性得到函数g(x)的奇偶性,由f(1)=0得g(1)=0、还有g(-1)=0,再通过奇偶性进行转化,利用单调性求出不等式得解集.
解答 解:设g(x)=xf(x),
则g'(x)=[xf(x)]'=x'f(x)+xf'(x)=f(x)+xf′(x)>0恒成立,
∴函数g(x)在区间(0,+∞)上是增函数,
∵f(x)是定义在R上的偶函数,∴g(x)=xf(x)是R上的奇函数,
∴函数g(x)在区间(-∞,0)上是增函数,
∵f(1)=0,∴f(-1)=0; 即g(-1)=0,g(1)=0
∴xf(x)>0化为g(x)>0,
当x>0时,不等式f(x)>0等价于g(x)>0,即g(x)>g(1),即x>1;
当x<0时,不等式f(x)>0等价于g(x)<0,即g(x)<g(-1),即x<-1.
故所求的解集为(-∞,-1)∪(1,+∞).
故选:C
点评 本题考查了由条件构造函数和用导函数的符号判断函数的单调性,利用函数的单调性和奇偶性的关系对不等式进行转化,注意函数值为零的自变量的取值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.在△ABC 中,∠A=60°,a=$\sqrt{13}$,b=4,则满足条件的△ABC ( )
| A. | 有两个 | B. | 有一个 | C. | 不存在 | D. | 有无数多个 |
3.在△ABC中,A=60°,b=1,这个三角形的面积为$\sqrt{3}$,则sin C的值为( )
| A. | $\frac{{\sqrt{3}}}{8}$ | B. | $\frac{{\sqrt{15}}}{8}$ | C. | $\frac{{2\sqrt{39}}}{13}$ | D. | $\frac{{\sqrt{3}}}{2}$ |

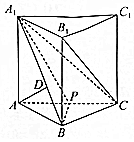 如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上,P为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上,P为AC的中点.