题目内容
17.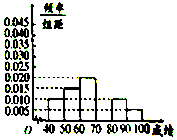 如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题:
如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图形的信息,回答下列问题:(1)求成绩在区间[70,80)内的频率,并补全这个频率分布直方图,并估计这次考试的及格率(60分及以上为及格);
(2)从成绩在[80,100]内的学生中选出三人,记在90分以上(含90分)的人数为X,求X的分布列及数学期望.
分析 (1)根据各组的频率和为1求出成绩在[70,80)内的频率,计算对应小矩形的高,补全频率分布直方图,再计算60分及以上分数的频率和即可;
(2)计算成绩在[80,90)和[90,100)内的人数,得X的可能取值,求出对应的概率值,写出X的分布列,计算数学期望.
解答 解:(1)根据各组的频率和等于1知,
成绩在[70,80)内的频率为:
f4=1-(0.01×2+0.015+0.020+0.005)×10=0.4,
对应的小矩形的高为$\frac{0.4}{10}$=0.04,
补全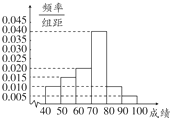 频率分布直方图如图所示;
频率分布直方图如图所示;
依题意,60分及以上的分数在第三、四、五、六段,
故其频率和为(0.02+0.04+0.01+0.005)×10=0.75,
∴估计学生成绩的及格率是75%;
(2)成绩在[80,100]内的人数为(0.01+0.005)×10×40=6,
且在[80,90)和[90,100)内的人数分别为4人和2人;
∴X的可能取值为0、1、2,
计算P(X=0)=$\frac{{C}_{4}^{3}{•C}_{2}^{0}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
P(X=1)=$\frac{{C}_{4}^{2}{•C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
P(X=2)=$\frac{{C}_{4}^{1}{•C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查了概率的求法与离散型随机变量的分布列和数学期望的计算问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知(1-x)10=a0+a1(1+x)+a2(1+x)2+…+a10(1+x)10,则a9=( )
| A. | -20 | B. | 20 | C. | -10 | D. | 10 |
2.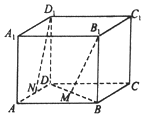 如图所示,在正方体ABCD-A1B1C1D1中,己知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,己知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
 如图所示,在正方体ABCD-A1B1C1D1中,己知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,己知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | -$\frac{\sqrt{15}}{15}$ | B. | $\frac{\sqrt{30}}{10}$ | C. | -$\frac{\sqrt{30}}{10}$ | D. | $\frac{\sqrt{15}}{15}$ |
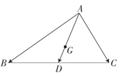
9.如图,G是△ABC的重心,D为BC的中点,$\overrightarrow{AB}+\overrightarrow{AC}$=λ$\overrightarrow{GD}$,则λ的值为( )

| A. | 3 | B. | 4 | C. | 6 | D. | 12 |
6.在△ABC 中,∠A=60°,a=$\sqrt{13}$,b=4,则满足条件的△ABC ( )
| A. | 有两个 | B. | 有一个 | C. | 不存在 | D. | 有无数多个 |