题目内容
14．在△ABC中，已知a=2，b=2$\sqrt{3}$，B=120°，解此三角形．分析 利用正弦定理列出关系式，求出sinA，确定出A的度数，进而求出C的度数，得到c的值．
解答 解：△ABC中，∵a=2，b=2$\sqrt{3}$，B=120°，
∴由正弦定理得：sinA=$\frac{asinB}{b}$=$\frac{1}{2}$，
∵a＜b，∴A=30°，
∴C=30°，c=a=2．
点评 此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键，属于基础题．
练习册系列答案
相关题目
4．已知正三棱柱ABC-A1B1C1的顶点A1，B1，C1在同一球面上，且平面ABC经过球心，若此球的表面积为4π，则该三棱柱的侧面积的最大值为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\sqrt{3}$ | C． | $\frac{3\sqrt{3}}{2}$ | D． | 3$\sqrt{3}$ |
2．
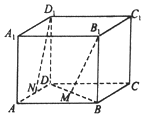如图所示，在正方体ABCD-A1B1C1D1中，己知棱长为a，M，N分别是BD和AD的中点，则B1M与D1N所成角的余弦值为（ ）
如图所示，在正方体ABCD-A1B1C1D1中，己知棱长为a，M，N分别是BD和AD的中点，则B1M与D1N所成角的余弦值为（ ）| A． | -$\frac{\sqrt{15}}{15}$ | B． | $\frac{\sqrt{30}}{10}$ | C． | -$\frac{\sqrt{30}}{10}$ | D． | $\frac{\sqrt{15}}{15}$ |
9．如图，G是△ABC的重心，D为BC的中点，$\overrightarrow{AB}+\overrightarrow{AC}$=λ$\overrightarrow{GD}$，则λ的值为（ ）
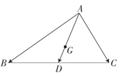
| A． | 3 | B． | 4 | C． | 6 | D． | 12 |
6．在△ABC 中，∠A=60°，a=$\sqrt{13}$，b=4，则满足条件的△ABC （ ）
| A． | 有两个 | B． | 有一个 | C． | 不存在 | D． | 有无数多个 |
3．在△ABC中，A=60°，b=1，这个三角形的面积为$\sqrt{3}$，则sin C的值为（ ）
| A． | $\frac{{\sqrt{3}}}{8}$ | B． | $\frac{{\sqrt{15}}}{8}$ | C． | $\frac{{2\sqrt{39}}}{13}$ | D． | $\frac{{\sqrt{3}}}{2}$ |