题目内容
已知数列{an}满足an＝logn＋1(n＋2)(n∈N*)，定义使a1·a2·a3·…·ak为整数的数k(k∈N*)叫做幸运数，则k∈[1,2 014]内所有的幸运数的和为( )
A．1 013 B．1 560
C．2 026 D．2 088
C
[解析] 由题可得a1·a2·a3·…·ak
＝log23·log34·log45·…·logk＋1(k＋2)
＝
·
·
·…·
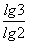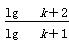
＝log2(k＋2)为整数，
即log2(k＋2)＝m，m∈Z，则k＝2m－2，结合k∈[1,2014]，则k∈{2,6,14,30,62,126,254,510,1 022}，所以2＋6＋14＋30＋62＋126＋254＋510＋1 022＝(22＋23＋…＋210)－18＝2 026，故选C.
练习册系列答案
相关题目
，且
，
、
的值； （2）当
时，求
的最大值
＋2sin x.
，求f(A)的值；
asin C－b－c＝0，则A＝________.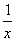
(x>0)的图象上．若点Bn的坐标为(n,0)(n≥2，n∈N*)，记矩形AnBnCnDn的周长为an，则a2＋a3＋…＋a10＝( )