题目内容
已知数列{an}的前n项和为Sn,且a1=0,对任意n∈N*,都有nan+1=Sn+n(n+1).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足an+log2n=log2bn,求数列{bn}的前n项和Tn.
解:(1)解法一:∵nan+1=Sn+n(n+1),
∴当n≥2时,(n-1)an=Sn-1+n(n-1),
两式相减,得nan+1-(n-1)an=Sn-Sn-1+n(n+1)-n(n-1),
即nan+1-(n-1)an=an+2n,化简,得an+1-an=2.
当n=1时,1×a2=S1+1×2,即a2-a1=2.
∴数列{an}是以0为首项,2为公差的等差数列.
∴an=2(n-1)=2n-2.
解法二:由nan+1=Sn+n(n+1),得
n(Sn+1-Sn)=Sn+n(n+1),
整理,得nSn+1=(n+1)Sn+n(n+1),
两边同除以n(n+1),得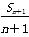 -
-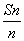 =1.
=1.
∴数列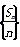 是以
是以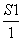 =0为首项,1为公差的等差数列.
=0为首项,1为公差的等差数列.
∴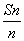 =0+n-1=n-1.
=0+n-1=n-1.
∴Sn=n(n-1).
当n≥2时,an=Sn-Sn-1=n(n-1)-(n-1)(n-2)=2n-2.
又a1=0适合上式,
∴数列{an}的通项公式为an=2n-2.
(2)∵an+log2n=log2bn,
∴bn=n·2an=n·22n-2=n·4n-1.
∴Tn=b1+b2+b3+…+bn-1+bn=40+2×41+3×42+…+(n-1)×4n-2+n×4n-1, ①
4Tn=41+2×42+3×43+…+(n-1)×4n-1+n×4n, ②
①-②,得-3Tn=40+41+42+…+4n-1-n·4n=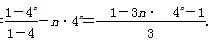
∴Tn=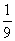 [(3n-1)·4n+1].
[(3n-1)·4n+1].

练习册系列答案
相关题目
 m3是时间t(s)的函数,则
m3是时间t(s)的函数,则 函数V=f(t)的解析式为_______
函数V=f(t)的解析式为_______ 时,就可起到保护作用.则当围栏的造价最低时,∠ABO=( )
时,就可起到保护作用.则当围栏的造价最低时,∠ABO=( )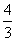 ,公比为-
,公比为- ,其前n项和为Sn,若A≤Sn-
,其前n项和为Sn,若A≤Sn-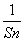 ≤B对任意n∈N*恒成立,则B-A的最小值为________.
≤B对任意n∈N*恒成立,则B-A的最小值为________.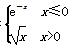 g(x)=f(x)-
g(x)=f(x)-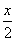 -b有且仅有一个零点时,b的取值范围是________.
-b有且仅有一个零点时,b的取值范围是________.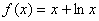 的零点所在的区间为( )
的零点所在的区间为( )