题目内容
若数列{an}的前n项和为Sn,有下列命题:
(1)若数列{an}是递增数列,则数列{Sn}也是递增数列;
(2)无穷数列{an}是递增数列,则至少存在一项ak,使得ak>0;
(3)若{an}是等差数列(公差d≠0),则S1·S2·…·Sk=0的充要条件是a1·a2·…·ak=0;
(4)若{an}是等比数列,则S1·S2·…·Sk=0(k≥2)的充要条件是an+an+1=0.
其中,正确命题的个数是( )
A.0 B.1
C.2 D.3
B
[解析] (1)错,例如:数列-3,-2,-1,0,1,2,3,Sn不是递增数列.(2)错,例如:an=-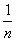 ,则{an}是递增数列,但an<0.(3)错,例如:等差数列-3,-2,-1,0,有a1·a2·a3·a4=0,而S1·S2·S3·S4≠0.(4)正确,若an+an+1=0,则q=-1,当k≥2时,一定会出现Sk=
,则{an}是递增数列,但an<0.(3)错,例如:等差数列-3,-2,-1,0,有a1·a2·a3·a4=0,而S1·S2·S3·S4≠0.(4)正确,若an+an+1=0,则q=-1,当k≥2时,一定会出现Sk= =0;若Sk=
=0;若Sk= =0,则qk=1.又q≠1,k≥2时,必有q=-1,故选B.
=0,则qk=1.又q≠1,k≥2时,必有q=-1,故选B.

练习册系列答案
相关题目
 ≤x≤2},B={x|0≤x≤4},则A∩B=______________
≤x≤2},B={x|0≤x≤4},则A∩B=______________ +2)ab.
+2)ab.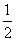 (ω>0)的相邻两个极值的横坐标分别为x0-
(ω>0)的相邻两个极值的横坐标分别为x0-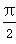 ,x0,求f(x)的单调递减区间.
,x0,求f(x)的单调递减区间.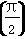 =( )
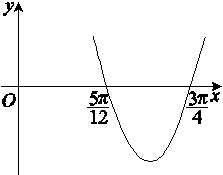
=( )
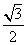 B.-
B.-