题目内容
函数f(x)= +2sin x.
+2sin x.
(1)在△ABC中,cos A=- ,求f(A)的值;
,求f(A)的值;
(2)求函数f(x)的最小正周期及其图象的所有对称轴的方程.
解:(1)由sin x+cos x≠0,得
x≠kπ- ,k∈Z.
,k∈Z.
 在△ABC中,cos A=-
在△ABC中,cos A=- <0,
<0,
所以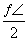 <A<π,
<A<π,
所以sin A= =
= ,
,
所以f(A)=sin A+cos A= -
- =
= .
.
(2)由(1),可得f(x)=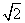 sin
sin ,
,
所以f(x)的最小正周期T=2π.
因为函数y=sin x图象的对称轴为x=kπ+ ,k∈Z,
,k∈Z,
又由x+ =kπ+
=kπ+ ,k∈Z,得x=kπ+
,k∈Z,得x=kπ+ ,k∈Z,
,k∈Z,
所以f(x)图象的所有对称轴的方程为x=kπ+ ,k∈Z.
,k∈Z.

练习册系列答案
相关题目
 间定义某种运算(用
间定义某种运算(用 表示):当
表示):当 ;当
;当 .在这种定义下,集合
.在这种定义下,集合 的元素个数为____________
的元素个数为____________ m3是时间t(s)的函数,则
m3是时间t(s)的函数,则 函数V=f(t)的解析式为_______
函数V=f(t)的解析式为_______ 的图象与函数f(x)的图象关于点(0,1)对称,则函数f(x)可由h(x)经过________的变换得到.( )
的图象与函数f(x)的图象关于点(0,1)对称,则函数f(x)可由h(x)经过________的变换得到.( )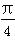 个单位
个单位  上有两个不同的实数解,则k的取值范围为________.
上有两个不同的实数解,则k的取值范围为________. 时,就可起到保护作用.则当围栏的造价最低时,∠ABO=( )
时,就可起到保护作用.则当围栏的造价最低时,∠ABO=( )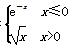 g(x)=f(x)-
g(x)=f(x)-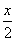 -b有且仅有一个零点时,b的取值范围是________.
-b有且仅有一个零点时,b的取值范围是________.