题目内容
已知函数f（x）的定义域为[3，6]，则函数y=
的定义域为（ ）
| f(2x) | ||||
|
A、[
| ||
B、[
| ||
C、（
| ||
D、[
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由函数的定义域得到2x的范围，根据分母不为0及被开方数非负得到关于x的不等式，求出不等式的解集．
解答：
解：由函数f（x）的定义域是[3，6]，得到3≤2x≤6，
故
解得：
≤x＜2；
所以原函数的定义域是：[
，2）．
故选：B
故
|
解得：
| 3 |
| 2 |
所以原函数的定义域是：[
| 3 |
| 2 |
故选：B
点评：此题考查学生掌握复合函数的定义域，考查了对数不等式的解法，是一道基础题．
练习册系列答案
相关题目
设函数f（x）=
则下列结论不正确的是（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
复数z=
（i是虚数单位）的虚部是（ ）
| 3-i |
| 1-i |
| A、2 | B、-2 | C、1 | D、-1 |
已知集合A={x∈R|
＜2x＜8}，B={x∈R|-2＜x≤4}，则A∩B等于（ ）
| 1 |
| 2 |
| A、（-1，3） | ||
| B、（-1，4） | ||
C、(
| ||
D、(
|
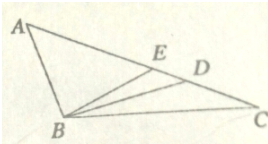在△ABC中，E为线段AC的中点，试问在线段AC上是否存在一点D．使得
如图，正方体的棱长a，点C，D分别是两条棱的中点．