题目内容
4.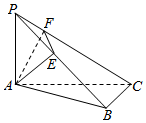 如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:
如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:(1)平面PAB⊥平面PBC;
(2)平面AEF⊥平面PBC;
(3)平面AEF⊥平面PAC.
分析 (1)由PA⊥平面ABC,得BC⊥PA,由∠ABC=90°,得BC⊥AB,从而可证BC⊥平面PAB,即可证明平面PAB⊥平面PBC;
(2)由BC⊥平面PAB,AE?平面PAB,可得BC⊥AE,由AE⊥PB于E,PB∩BC=B,得AE⊥平面PBC,从而可证平面AEF⊥平面PBC;
(3)由AE⊥平面PBC,得AE⊥PC,由AF⊥PC,AF∩AE=A,得PC⊥平面AEF,从而可证平面AEF⊥平面PAC.
解答 证明:(1)∵PA⊥平面ABC,∴BC⊥PA
∵∠ABC=90°,∴BC⊥AB
∵PA∩AB=A
∴BC⊥平面PAB,
∵BC?平面PBC,
∴平面PAB⊥平面PBC;
(2)∵BC⊥平面PAB,AE?平面PAB
∴BC⊥AE
∵AE⊥PB于E,PB∩BC=B
∴AE⊥平面PBC,
∵AE?平面AEF,
∴平面AEF⊥平面PBC
(3)∵AE⊥平面PBC
∴AE⊥PC
∵AF⊥PC,AF∩AE=A
∴PC⊥平面AEF
∵PC?平面PAC
∴平面AEF⊥平面PAC.
点评 本题主要考查了平面与平面垂直的判定,直线与平面垂直的判定,属于基本知识的考查.

练习册系列答案
相关题目
14.锐角△ABC中,a,b,c分别是角A,B,C的对边,若B=2A,则$\frac{b}{a}$的取值范围是( )
| A. | (0,2) | B. | ($\sqrt{2}$,2) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{3}$,2) |
16.从6名男同学和4名女同学中,选出3名男同学和2名女同学的担任五种不同的职务,不同的分配方案有( )种.
| A. | ${C}_{6}^{3}{C}_{4}^{2}$ | B. | ${A}_{6}^{3}{A}_{4}^{2}$ | C. | ${C}_{6}^{3}{C}_{4}^{2}{A}_{5}^{5}$ | D. | $({C}_{6}^{3}+{C}_{4}^{2}){A}_{5}^{5}$ |
16.设全集U=R,集合A={x|1<2x<4},B={x|log2x>0},则(∁UA)∩B=( )
| A. | [2,+∞) | B. | (1,2] | C. | (-∞,0]∪[2,+∞) | D. | (-∞,0]∪(1,+∞) |