题目内容
16.设全集U=R,集合A={x|1<2x<4},B={x|log2x>0},则(∁UA)∩B=( )| A. | [2,+∞) | B. | (1,2] | C. | (-∞,0]∪[2,+∞) | D. | (-∞,0]∪(1,+∞) |
分析 利用对数与指数函数的性质分别求出A与B中不等式的解集确定出A与B,找出A补集与B的交集即可.
解答 解:由A中不等式变形得:20=1<2x<4=22,即0<x<2,
∴A=(0,2),
∵全集U=R,∴∁UA=(-∞,0]∪[2,+∞),
由B中不等式变形得:log2x>0=log21,得到x>1,即B=(1,+∞),
则(∁UA)∩B=[2,+∞),
故选:A.
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
4.用二分法研究函数f(x)=x5+8x3-1的零点时,第一次经过计算f(0)<0,f(0.5)>0,则其中一个零点所在的区间和第二次应计算的函数值分别为( )
| A. | (0,0.5)f(0.125) | B. | (0.5,1)f(0.25) | C. | (0.5,1)f(0.75) | D. | (0,0.5)f(0.25) |
11.下列关系正确的是( )
| A. | 0∉N | B. | 0•$\overrightarrow{AB}$=0 | ||
| C. | cos0.75°>cos0.75 | D. | lge>(lge)2>lg$\sqrt{e}$ |
1.已知f(x)=|x|-1,关于x的方程f2(x)-|f(x)|+k=0,则下列四个结论错误的是( )
| A. | 存在实数k,使方程恰有2个不同的实根 | |
| B. | 存在实数k,使方程恰有3个不同的实根 | |
| C. | 存在实数k,使方程恰有5个不同的实根 | |
| D. | 存在实数k,使方程恰有8个不同的实根 |
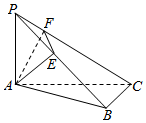 如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:
如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证: