题目内容
19.不解三角形,判断下列三角形解的个数.(1)a=5,b=4,A=120°;
(2)a=7,b=14,A=150°;
(3)a=9,b=10,A=60°.
分析 根据正弦定理判断两边所对角的大小关系,结合三角形的内角和定理得出结论.
解答 解:(1)由b<a可知sinB<sinA=sin60,故B<60°,从而三角形只有一解.
(2)根据正弦定理得:$\frac{7}{sin150°}$=$\frac{14}{sinB}$,解得sinB=1,B为直角,所以此三角形无解.
(3)bsinA=5$\sqrt{3}$,∵bsinA<a<b,∴三角形有两解.
点评 本题考查了正弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
9.已知0<x<8,则x(8-x)的最大值是( )
| A. | 7 | B. | 12 | C. | 15 | D. | 16 |
11.甲、乙两位同学各拿出4本书,用作投骰子的奖品,两人商定:骰子朝上的面点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜得所有8本书,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后也们不想再继续这场游戏,下面对这8本书分配台理的是( )
| A. | 甲得6本,乙得2本 | B. | 甲得5本,乙得3本 | C. | 甲得4本,乙得4本 | D. | 甲得7本,乙得1本 |
11.下列关系正确的是( )
| A. | 0∉N | B. | 0•$\overrightarrow{AB}$=0 | ||
| C. | cos0.75°>cos0.75 | D. | lge>(lge)2>lg$\sqrt{e}$ |
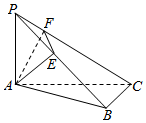 如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:
如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证: