题目内容
13.已知f(x)是偶函数,且x≥0时,f(x)=2x-x2,则当x<0时,f(x)的解析式为f(x)=-x2-2x.分析 设x<0,则-x>0,从而利用条件当x≥0时,f(x)=-x2+2x,结合f(x)为偶函数,即可求得f(x)在R上的解析式.
解答 解:设x<0,则-x>0,
∴f(-x)=2(-x)-(-x)2=-x2-2x
又∵f(x)为偶函数,
∴f(-x)=f(x),
∴f(x)=-x2-2x,
故答案为:f(x)=-x2-2x.
点评 本题重点考查函数解析式的求解,考查偶函数性质的运用,是一道基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
4.用二分法研究函数f(x)=x5+8x3-1的零点时,第一次经过计算f(0)<0,f(0.5)>0,则其中一个零点所在的区间和第二次应计算的函数值分别为( )
| A. | (0,0.5)f(0.125) | B. | (0.5,1)f(0.25) | C. | (0.5,1)f(0.75) | D. | (0,0.5)f(0.25) |
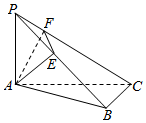 如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证:
如图,P为△ABC所在平面外一点,PA⊥平面ABC,∠ABC=90°,AE⊥PB于E,AF⊥PC于F,求证: