题目内容
若函数f(x)=loga(2x+1)(a>0,且a≠1)在区间(-
,0)内恒有f(x)>0,则f(x)的单调减区间是( )
| 1 |
| 2 |
A、(-∞,-
| ||
B、(-
| ||
| C、(-∞,0) | ||
| D、(0,+∞) |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:由条件f(x)>0判断出a的范围,再根据复合函数“同增异减”原则求f(x)单调区间.
解答:
解:函数f(x)=loga(2x+1)的定义域为(-
,+∞),
当x∈(-
,0)时,2x+1∈(0,1),∴0<a<1,
∵函数f(x)=loga(2x+1)(a>0,a≠1)由f(x)=logat和t=x+1复合而成,
0<a<1时,f(x)=logat在(0,+∞)上是减函数,而t=x+1为增函数,
∴f(x)在其定义域内单调递减,
∵函数f(x)=loga(2x+1)的定义域为(-
,+∞),
∴f(x)的单调减区间是(-
,+∞).
故选:B.
| 1 |
| 2 |
当x∈(-
| 1 |
| 2 |
∵函数f(x)=loga(2x+1)(a>0,a≠1)由f(x)=logat和t=x+1复合而成,
0<a<1时,f(x)=logat在(0,+∞)上是减函数,而t=x+1为增函数,
∴f(x)在其定义域内单调递减,
∵函数f(x)=loga(2x+1)的定义域为(-
| 1 |
| 2 |
∴f(x)的单调减区间是(-
| 1 |
| 2 |
故选:B.
点评:本题考查复合函数的单调区间问题,复合函数的单调区间复合“同增异减”原则,在解题中勿忘真数大于0条件.

练习册系列答案
相关题目
用数学归纳法证明2n>n2(n∈N*,n≥5)成立时,第二步归纳假设正确写法( )
| A、假设n=k时命题成立 |
| B、假设n=k(k∈N*)时命题成立 |
| C、假设n=k(n≥5)时命题成立 |
| D、假设n=k(n>5)时命题成立 |
不等式2x2-3|x|-35>0的解集为( )
A、{x|x<-
| ||
B、{x|0<x<
| ||
| C、{x|x<5或x>7} | ||
| D、{x|x<-5或x>5} |
若函数f(x)=
(a,b,c,d∈R)的图象如图所示,则a:b:c:d=( )
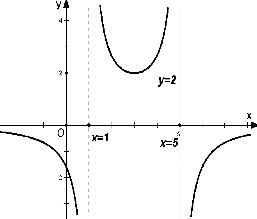
| d |
| ax2+bx+c |

| A、1:6:5:8 |
| B、1:6:5:(-8) |
| C、1:(-6):5:8 |
| D、1:(-6):5:(-8) |
已知y=
x3+bx2+(b+2)x+3在R上是增函数,则b的取值范围为( )
| 1 |
| 3 |
| A、(-1,2) |
| B、[-1,2] |
| C、(-2,1) |
| D、[-2,1] |
已知等差数列{an}的前n项和为Sn,且a3+a5+2a10=4,则S13的值为( )
| A、13 | B、26 | C、8 | D、162 |
与圆x2+y2-4y=0外切,又与x轴相切的圆的圆心轨迹方程是( )
| A、y2=8x |
| B、y2=8x(x>0)和y=0 |
| C、x2=8y(y>0) |
| D、x2=8y(y>0)和x=0(y<0) |