题目内容
已知在△ABC中，A=60°，最大边和最小边的长是方程3x2-27x+32=0的两实根，那么边BC的长为 ．
考点：余弦定理
专题：计算题,解三角形
分析：利用一元二次方程的根与系数的关系，得出最大边与最小边之间的等量关系，再利用三角形三边关系求出．
解答：
解：易知，a既不是最大边，也不是最小边，不妨假设c为最大边，b为最小边，则
∴a2=b2+c2-2bccos60°=（b+c）2-3bc=49
∴a=7（a=-7舍去）
故答案为：7
|
∴a2=b2+c2-2bccos60°=（b+c）2-3bc=49
∴a=7（a=-7舍去）
故答案为：7
点评：此题主要考查了一元二次方程根与系数的关系和三角形三边关系，以及二次根式的计算，题目综合性较强．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
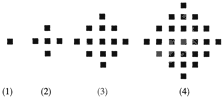某少数民族的刺绣有着悠久的历史，下图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．（理科）已知-3＜a＜2，3＜b＜4，则
的取值范围为（ ）
| a |
| b |
A、（-1，
| ||||
B、（-
| ||||
C、（-1，
| ||||
D、（-
|