题目内容
已知△ABC中,AC=1,∠ABC=
,∠BAC=x,记f(x)=
•
.
(1)求f(x)解析式并标出其定义域;
(2)设g(x)=6mf(x)+1(m<0),若g(x)的值域为[-
,1),求实数m的值.
| 2π |
| 3 |
| AB |
| BC |
(1)求f(x)解析式并标出其定义域;
(2)设g(x)=6mf(x)+1(m<0),若g(x)的值域为[-
| 3 |
| 2 |
考点:正弦定理的应用,三角函数中的恒等变换应用
专题:三角函数的求值,解三角形
分析:(1)由正弦定理有:
=
=
;利用数量积定义可得f(x)=
•
=
sinxsin(
-x)×
,化简即可;
(2)利用正弦函数的单调性即可得出.
| BC |
| sinx |
| 1 | ||
sin
|
| AB | ||
sin(
|
| AB |
| BC |
| 4 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
(2)利用正弦函数的单调性即可得出.
解答:
解:(1)由正弦定理有:
=
=
;
∴BC=
sinx,AB=
sin(
-x);
∴f(x)=
•
=
sinxsin(
-x)×
=
(
cosx-
sinx)sinx
=
sin(2x+
)-
(0<x<
).
(2)g(x)=6mf(x)+1=2msin(2x+
)-m+1,
∵x∈(0,
),
∴
<2x+
<
,
则sin(2x+
)∈(
,1].
当m<0时,g(x)=2msin(2x+
)-m+1的值域为[m+1,1].
又g(x)的值域为[-
,1),解得m=-
.
∴综上:m=-
.
| BC |
| sinx |
| 1 | ||
sin
|
| AB | ||
sin(
|
∴BC=
2
| ||
| 3 |
2
| ||
| 3 |
| π |
| 3 |
∴f(x)=
| AB |
| BC |
| 4 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| π |
| 6 |
| 1 |
| 6 |
| π |
| 3 |
(2)g(x)=6mf(x)+1=2msin(2x+
| π |
| 6 |
∵x∈(0,
| π |
| 3 |
∴
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
则sin(2x+
| π |
| 6 |
| 1 |
| 2 |
当m<0时,g(x)=2msin(2x+
| π |
| 6 |
又g(x)的值域为[-
| 3 |
| 2 |
| 5 |
| 2 |
∴综上:m=-
| 5 |
| 2 |
点评:本题考查了正弦定理、数量积定义、正弦函数的单调性、两角和差的正弦公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
若变量x,y满足约束条件
,则z=7x+2y的最大值是( )
|
| A、27 | B、19 | C、13 | D、9 |
曲线y=2x-x3在x=-1处的切线方程为( )
| A、x-y+2=0 |
| B、x+y-2=0 |
| C、x+y+2=0 |
| D、x-y-2=0 |
函数y=
+
是( )
| 1-|x| |
| 9 |
| 1+x2 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |

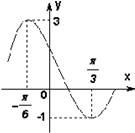 已知三角函数f(x)=Acos(ωx+φ)+b(A>ω>0,|φ|<
已知三角函数f(x)=Acos(ωx+φ)+b(A>ω>0,|φ|<