题目内容
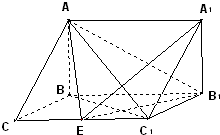 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=| π |
| 3 |
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1;
(Ⅲ)在(Ⅱ)的条件下,求AE和平面ABC所成角正弦值的大小.
考点:直线与平面所成的角,直线与平面垂直的判定,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)要证明C1B⊥平面ABC,根据本题条件,需要证明BC1⊥AB,由AB⊥侧面BB1C1C就可以解决;而要证明C1B⊥BC,则需要通过解三角形来证明;
(Ⅱ)要确定E点的位置,使得EA⊥EB1,由三垂线定理,必有BE⊥B1E,通过解直角三角形BEB1解决;
(Ⅲ)证明侧面BB1C1C⊥平面ABC1,过E做BC1的垂线交BC1于F,则EF⊥平面ABC1,连接AF,可得∠EAF为AE和平面ABC所成角.
(Ⅱ)要确定E点的位置,使得EA⊥EB1,由三垂线定理,必有BE⊥B1E,通过解直角三角形BEB1解决;
(Ⅲ)证明侧面BB1C1C⊥平面ABC1,过E做BC1的垂线交BC1于F,则EF⊥平面ABC1,连接AF,可得∠EAF为AE和平面ABC所成角.
解答:
 (Ⅰ)证明:∵BC=1,∠BCC1=
(Ⅰ)证明:∵BC=1,∠BCC1=
,CC1=2
∴由余弦定理可得BC1=
,
∴BC2+
=
,
∴BC1⊥BC.
∵AB⊥侧面BB1C1C,BC1?平面BB1C1C,
∴BC1⊥AB 且BC∩AB=B
∴C1B⊥平面ABC;------(4分)
(Ⅱ)解:连接BE,EA⊥EB1,AB⊥EB1,AB∩AE=A,AB,AE?平面ABE,
从而B1E⊥平面ABE,且BE?平面ABE,故BE⊥B1E,
不妨设CE=x,则C1E=2-x,则BE2=1+x2-x,
又∵∠B1C1C=
,则B1E2=1+x2+x,
在Rt△BEB1中有x2+x+1+x2-x+1=4,从而x=±1(舍负),
故E为CC1的中点时,EA⊥EB1;------(8分)
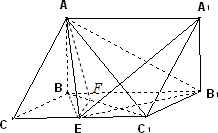
(Ⅲ)解:∵AB⊥侧面BB1C1C,AB?平面ABC1,
∴侧面BB1C1C⊥平面ABC1,
过E做BC1的垂线交BC1于F,则EF⊥平面ABC1,连接AF,
∴∠EAF为AE和平面ABC所成角.
∵BC⊥BC1,EF⊥BC1,
∴BC∥EF,
∵E为C1C的中点,
∴F为C1B的中点,
∴EF=
,
由(Ⅱ)知AE=
,
∴sin∠EAF=
=
------(14分)
 (Ⅰ)证明:∵BC=1,∠BCC1=
(Ⅰ)证明:∵BC=1,∠BCC1=| π |
| 3 |
∴由余弦定理可得BC1=
| 3 |
∴BC2+
| BC | 2 1 |
| CC | 2 1 |
∴BC1⊥BC.
∵AB⊥侧面BB1C1C,BC1?平面BB1C1C,
∴BC1⊥AB 且BC∩AB=B
∴C1B⊥平面ABC;------(4分)
(Ⅱ)解:连接BE,EA⊥EB1,AB⊥EB1,AB∩AE=A,AB,AE?平面ABE,
从而B1E⊥平面ABE,且BE?平面ABE,故BE⊥B1E,
不妨设CE=x,则C1E=2-x,则BE2=1+x2-x,
又∵∠B1C1C=
| 2π |
| 3 |
在Rt△BEB1中有x2+x+1+x2-x+1=4,从而x=±1(舍负),
故E为CC1的中点时,EA⊥EB1;------(8分)
(Ⅲ)解:∵AB⊥侧面BB1C1C,AB?平面ABC1,
∴侧面BB1C1C⊥平面ABC1,
过E做BC1的垂线交BC1于F,则EF⊥平面ABC1,连接AF,
∴∠EAF为AE和平面ABC所成角.
∵BC⊥BC1,EF⊥BC1,
∴BC∥EF,
∵E为C1C的中点,
∴F为C1B的中点,
∴EF=
| 1 |
| 2 |
由(Ⅱ)知AE=
| 5 |
∴sin∠EAF=
| ||
|
| ||
| 10 |
点评:本题考查线面垂直、线线垂直,考查线面角的求法,考查学生分析解决问题的能力,考查学生的计算能力,正确运用线面垂直的判定定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知三角形的三条边成公差为2的等差数列,且它的最大角的正弦值为
,则这个三角形的面积是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 矩形ABCD的中心在坐标原点,边AB与x轴平行,AB=8,BC=6.E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,R′,S′,T′是线段CF的四等分点.设直线ER与GR′,ES与GS′,ET与GT′的交点依次为L,M,N.
矩形ABCD的中心在坐标原点,边AB与x轴平行,AB=8,BC=6.E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,R′,S′,T′是线段CF的四等分点.设直线ER与GR′,ES与GS′,ET与GT′的交点依次为L,M,N.