题目内容
已知集合A={x|a-1＜x＜2a+1}，B={x|0＜x＜5}，若A∪B=B，求实数a的取值范围．
考点：并集及其运算
专题：集合
分析：由A∪B=B说明集合A是集合B的子集，当集合A是空集时，符合题目条件，求出此时的a的范围，当A不是空集时，由两集合端点值之间的关系列不等式组求出a的范围，最后把两种情况求出的a的范围取并集即可．
解答：
解：当A=∅时，有2a+1≤a-1，解得a≤-2…（4分）
当A≠∅时，有
…（8分）
解得1≤a≤2…（10分）
综上所述，实数a的取值范围为（-∞，-2]∪[1，2]…（12分）
当A≠∅时，有
|
解得1≤a≤2…（10分）
综上所述，实数a的取值范围为（-∞，-2]∪[1，2]…（12分）
点评：本题考查了并集及其运算，考查了集合之间的关系，考查了分类讨论的数学思想，解答此题的关键是由集合之间的关系得出它们的端点值之间的关系，是基础题也是易错题．
练习册系列答案
相关题目
已知角α的终边与单位圆x2+y2=1交于点P（
，y），则sin（
+α）=（ ）
| 1 |
| 2 |
| π |
| 2 |
| A、1 | ||||
B、
| ||||
C、-
| ||||
D、-
|
等比数列{an}中，a1=2，q=3，则an等于（ ）
| A、6 |
| B、3×2n-1 |
| C、2×3n-1 |
| D、6n |
函数y=tan（x-2）的最小正周期是（ ）
| A、π | ||
| B、2π | ||
C、
| ||
| D、1 |
曲线y=sinx在x=
处的切线方程是（ ）
| π |
| 2 |
| A、y=0 | B、y=x+1 |
| C、y=x | D、y=1 |
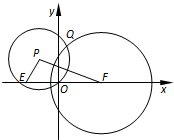如图，已知O（0，0），E（-
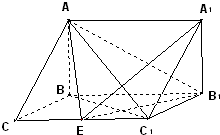在三棱拄ABC-A1B1C1中，AB⊥侧面BB1C1C，已知BC=1，∠BCC1=