题目内容
袋中有4个红球,3个黑球,从袋中随机取球,设取到一个红球得2分,取到一个黑球得1分,从袋中任取4个球,
(1)求得分X的分布列和数学期望;
(2)求得分大于6分的概率.
(1)求得分X的分布列和数学期望;
(2)求得分大于6分的概率.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)由题设知,X的可能取值为5,6,7,8,由题设条件利用排列组合知识分别求出P(X=5),P(X=6),P(X=7),P(X=8),由此能求出得分X的分布列和数学期望.
(2)由(1)知,得分大于6分的概率:P=P(X=7)+P(X=8),由此能求出结果.
(2)由(1)知,得分大于6分的概率:P=P(X=7)+P(X=8),由此能求出结果.
解答:
解:(1)由题设知,X的可能取值为5,6,7,8,
P(X=5)=
=
,
P(X=6)=
=
,
P(X=7)=
=
,
P(X=8)=
=
,
∴X的分布列为:
EX=5×
+6×
+7×
+8×
=
.
(2)由(1)知,得分大于6分的概率:
P=P(X=7)+P(X=8)=
+
=
.
P(X=5)=
| ||||
|
| 4 |
| 35 |
P(X=6)=
| ||||
|
| 18 |
| 35 |
P(X=7)=
| ||||
|
| 12 |
| 35 |
P(X=8)=
| ||||
|
| 1 |
| 35 |
∴X的分布列为:
| X | 5 | 6 | 7 | 8 | ||||||||
| P |
|
|
|
|
| 4 |
| 35 |
| 18 |
| 35 |
| 12 |
| 35 |
| 1 |
| 35 |
| 44 |
| 7 |
(2)由(1)知,得分大于6分的概率:
P=P(X=7)+P(X=8)=
| 12 |
| 35 |
| 1 |
| 35 |
| 13 |
| 35 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望,是中档题,解题时要合理运用排列组合知识.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
对集合A={1,2},B={1,2,3}及平面上的点M(a,b)(a∈A,b∈B),记“点M(a,b)落在直线x+y=3或x+y=4上”为事件P,则事件P发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知曲线y=
x3+
x2+4x-7在点Q处的切线的倾斜角α满足sin2α=
,则此切线的方程为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 17 |
A、4x-y+7=0或4x-y-6
| ||
B、4x-y-6
| ||
C、4x-y-7=0或4x-y-6
| ||
| D、4x-y-7=0 |
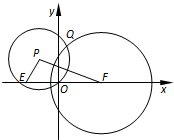 如图,已知O(0,0),E(-
如图,已知O(0,0),E(-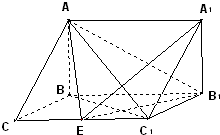 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=