题目内容
 矩形ABCD的中心在坐标原点,边AB与x轴平行,AB=8,BC=6.E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,R′,S′,T′是线段CF的四等分点.设直线ER与GR′,ES与GS′,ET与GT′的交点依次为L,M,N.
矩形ABCD的中心在坐标原点,边AB与x轴平行,AB=8,BC=6.E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,R′,S′,T′是线段CF的四等分点.设直线ER与GR′,ES与GS′,ET与GT′的交点依次为L,M,N.(1)求以HF为长轴,以EG为短轴的椭圆Q的方程;
(2)根据条件可判定点L,M,N都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段OF的n(n∈N+,n≥2)等分点从左向右依次为Ri(i=1,2,…,n-1),线段CF的n等分点从上向下依次为Ti(i=1,2,…,n-1),那么直线ERi(i=1,2,…,n-1)与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由题意,2a=AB=8,2b=BC=6,求出a,b,即可得出椭圆Q的方程;
(2)确定直线ER的方程、直线GR′的方程,联立可解得L的坐标,代入椭圆方程,即可得证.
(3)由(2)知,直线ERi(i=1,2,…,n-1)与直线GTi(i=1,2,…,n-1)的交点一定在椭圆Q上.
(2)确定直线ER的方程、直线GR′的方程,联立可解得L的坐标,代入椭圆方程,即可得证.
(3)由(2)知,直线ERi(i=1,2,…,n-1)与直线GTi(i=1,2,…,n-1)的交点一定在椭圆Q上.
解答:
解:(1)由题意,2a=AB=8,2b=BC=6,
∴a=4,b=3,
∴椭圆Q的方程为
+
=1;
(2)由题意知E(0,-3),R(1,0),G(0,3),R(4,
).
可得直线ER的方程为y=3x-3,直线GR′的方程为y=-
x+3
联立可解得L(
,
),代入椭圆方程
+
=1成立,得证.
(3)由(2)知,直线ERi(i=1,2,…,n-1)与直线GTi(i=1,2,…,n-1)的交点一定在椭圆Q上.
∴a=4,b=3,
∴椭圆Q的方程为
| x2 |
| 16 |
| y2 |
| 9 |
(2)由题意知E(0,-3),R(1,0),G(0,3),R(4,
| 9 |
| 4 |
可得直线ER的方程为y=3x-3,直线GR′的方程为y=-
| 3 |
| 16 |
联立可解得L(
| 96 |
| 51 |
| 135 |
| 51 |
| x2 |
| 16 |
| y2 |
| 9 |
(3)由(2)知,直线ERi(i=1,2,…,n-1)与直线GTi(i=1,2,…,n-1)的交点一定在椭圆Q上.
点评:本题考查椭圆的标准方程,考查直线焦点坐标的求法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
等比数列{an}中,a1=2,q=3,则an等于( )
| A、6 |
| B、3×2n-1 |
| C、2×3n-1 |
| D、6n |
过点(3,0)和点(4,
)的直线的倾斜角是( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
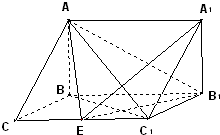 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=