题目内容
设函数f(x)=
-
sin2x.
(1)求函数f(x)的最小正周期和对称中心;
(2)设函数g(x)对任意x∈R,有g(x+
)=g(x),且当x∈[0,
]时,g(x)=
-f(x),求函数g(x)在[-π,0]上的解析式.
(3)在(2)的条件下,若对任意的x1∈[
,任意的x2∈[-
,都有f(x1)>g(x2)+m,求m的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期和对称中心;
(2)设函数g(x)对任意x∈R,有g(x+
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
(3)在(2)的条件下,若对任意的x1∈[
| π |
| 6 |
| π |
| 3 |
考点:三角函数的最值,正弦函数的图象
专题:计算题,三角函数的图像与性质
分析:(1)利用正弦函数的最小正周期以及函数的对称中心直接求解函数f(x)的最小正周期和对称中心;
(2)通过g(x+
)=g(x),得到函数的周期,利用函数解析式的求法求解当x∈[0,
]时,g(x)=
-f(x),函数g(x)在[-π,0]上的解析式.
(3)对任意的x1∈[
,任意的x2∈[-
,都有f(x1)>g(x2)+m,转化为f(x)min>[g(x)+m]max,求出两个函数的最值,即可求m的取值范围.
(2)通过g(x+
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
(3)对任意的x1∈[
| π |
| 6 |
| π |
| 3 |
解答:
解:(1)函数f(x)的最小正周期为T=
=π,
令2x=kπ,k∈Z,得x=
,k∈Z
所以对称中心为(
,
)k∈Z.;
(2)函数g(x)对任意x∈R,有g(x+
)=g(x),
∴函数g(x)的周期为:
,
当x∈[0,
]时,g(x)=
-f(x)=
sin2x,
当x∈[-π,-
]时,x+π∈[0,
],g(x+π)=g(x),
∴函数g(x)=
sin(2x+2π)=
sin2x
当x∈[-
,0]时,x+
∈[0,
],g(x+
)=g(x)
∴函数g(x)=
sin(2x+π)=-
sin2x.
∴函数g(x)在[-π,0]上的解析式为:g(x)=
.
(3)对任意的x1∈[
,任意的x2∈[-
,
都有f(x1)>g(x2)+m,
就是f(x)min>[g(x)+m]max,
对任意的x1∈[
,函数f(x)=
-
sin2x的最小值为:
-
×sin
=0.
x2∈[-
,g(x)+m=-
sin2x+m的最大值为:1+m,
∴0>1+m.∴m<-1.
m的取值范围:(-∞,-1).
| 2π |
| 2 |
令2x=kπ,k∈Z,得x=
| kπ |
| 2 |
所以对称中心为(
| kπ |
| 2 |
| 1 |
| 2 |
(2)函数g(x)对任意x∈R,有g(x+
| π |
| 2 |
∴函数g(x)的周期为:
| π |
| 2 |
当x∈[0,
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x∈[-π,-
| π |
| 2 |
| π |
| 2 |
∴函数g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
当x∈[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴函数g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
∴函数g(x)在[-π,0]上的解析式为:g(x)=
|
(3)对任意的x1∈[
| π |
| 6 |
| π |
| 3 |
都有f(x1)>g(x2)+m,
就是f(x)min>[g(x)+m]max,
对任意的x1∈[
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
x2∈[-
| π |
| 3 |
| 1 |
| 2 |
∴0>1+m.∴m<-1.
m的取值范围:(-∞,-1).
点评:本题考查三角函数的最值的应用,正弦函数的对称性与周期性,考查函数的解析式的求法,基本知识的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列四个命题中正确的是( )
| A、公比q>1的等比数列的各项都大于1 |
| B、公比q<0的等比数列是递减数列 |
| C、常数列是公比为1的等比数列 |
| D、{lg2n}是等差数列而不是等比数列 |
函数y=tan(x-2)的最小正周期是( )
| A、π | ||
| B、2π | ||
C、
| ||
| D、1 |
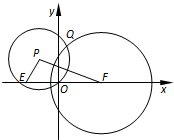 如图,已知O(0,0),E(-
如图,已知O(0,0),E(-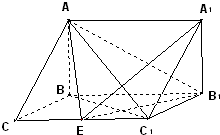 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=