题目内容
已知三角形的三条边成公差为2的等差数列,且它的最大角的正弦值为
,则这个三角形的面积是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:等差数列的性质
专题:等差数列与等比数列
分析:由题意设出三角形的三边,由最大角大于60°及其正弦值为
得其余弦值,然后代入余弦定理求解三边,进一步代入三角形的面积公式得答案.
| ||
| 2 |
解答:
解:由题意设三角形的三边x-2,x,x+2,
最大角为A,A>60°,则sinA=
,cosA=-
.
由三角形两边之和大于第三边知,x+(x-2)>x+2,即x>4,
由预先定理得:cosA=
=
=
=-
即2(x-8)=-2x+4,解得:x=5.
∴三角形的三边分别为3,5,7.
该三角形的面积为:
×3×5×sinA=
×3×5×
=
.
故选:B.
最大角为A,A>60°,则sinA=
| ||
| 2 |
| 1 |
| 2 |
由三角形两边之和大于第三边知,x+(x-2)>x+2,即x>4,
由预先定理得:cosA=
| x2+(x-2)2-(x+2)2 |
| 2x(x-2) |
| x2-8x |
| 2x(x-2) |
| x-8 |
| 2x-4 |
| 1 |
| 2 |
即2(x-8)=-2x+4,解得:x=5.
∴三角形的三边分别为3,5,7.
该三角形的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
15
| ||
| 4 |
故选:B.
点评:本题考查了等差数列的性质,考查了余弦定理在解三角形中的应用,是中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知角α的终边与单位圆x2+y2=1交于点P(
,y),则sin(
+α)=( )
| 1 |
| 2 |
| π |
| 2 |
| A、1 | ||||
B、
| ||||
C、-
| ||||
D、-
|
下列四个命题中正确的是( )
| A、公比q>1的等比数列的各项都大于1 |
| B、公比q<0的等比数列是递减数列 |
| C、常数列是公比为1的等比数列 |
| D、{lg2n}是等差数列而不是等比数列 |
log39=( )
| A、1 | ||
| B、2 | ||
| C、3 | ||
D、
|
对集合A={1,2},B={1,2,3}及平面上的点M(a,b)(a∈A,b∈B),记“点M(a,b)落在直线x+y=3或x+y=4上”为事件P,则事件P发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
等比数列{an}中,a1=2,q=3,则an等于( )
| A、6 |
| B、3×2n-1 |
| C、2×3n-1 |
| D、6n |
函数y=tan(x-2)的最小正周期是( )
| A、π | ||
| B、2π | ||
C、
| ||
| D、1 |
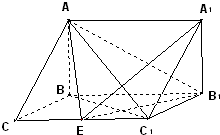 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=